3 Jakaumat ja odotusarvo
Edellisessä kappaleessa tutkimme nopanheiton pistesumman jakaumaa. Kokosimme sen alkaistapahtumista käsin. Vaikka aineistoja analysoitaessa jakaumat määrittyvät havainnoista todennäköisyysmallin sijaan, on silti hyödyllistä miettiä taustalla olevaa mallia ja piileviksi jääviä alkeistapahtumia. Ne ovat syy miksi aineisto jakaantuu, kuten tekee.
3.1 Empiirisiä esimerkkijakaumia
3.1.1 Diskreetit ja jatkuvat jakaumat
Kenties yksinkertaisin ei-triviaali jakauma on kaksiluokkaisen satunnaismuuttujan jakauma. Esimerkiksi tästä käy kolikon heitto, jossa kruunan todennäköisyys on \(p\) ja klaavan \(1 - p\). Jos kolikko on “reilu”, \(p = 0.5\). Jollei tällaistä oletusta voida tehdä, arvo \(p \in [0, 1]\) on tuntematon. Se voidaan estimoida aineistosta heittämällä kolikkoa monta kertaa ja olettamalla todennäköisyysmallin pysyvän vakiona (palaamme estimointiin myöhemmin tarkemmin). Tämä edustaa induktiivista päättelyä. Vaihtoehtoisesti arvo \(p\) voidaan pyrkiä laskemaan deduktiivisesti kolikon ominaisuuksista ja fysiikan laeista päättelemällä. Itse asiassa “reiluusoletus” edustaa jälkimmäistä strategiaa. Samankaltaista todennäköisyysmallia sovelletaan tyypillisesti myös muuttujiin, joille deduktiivinen strategia on täysin mahdoton. Esimerkiksi, \(p\) saattaa edustaa osuutta jonkin väestön henkilöistä, joilla on uniongelmia. Tällöin on tärkeää viitata väestöjakaumaan. Sillekin voidaan ajatella olevan olemassa jokin todennäköisyysmalli, joltain alkeistapahtumilta todennäköisyyksille \((p_1, p_2, ..., p_n)\). Voimme estimoida uniongelmien suhteellisen osuuden havaitussa väestössä,
\[ \hat{p} = \frac{1}{n} \sum_{i = 1}^n 1_{ \{ \text{hlö } i \text{ uniongelmainen} \} }, \]
missä \(1_{A} = 1\), kun \(A\) pätee ja \(1_{A} = 0\) muulloin. Toisin kuin kolikon tapauksessa, oletusta \(\hat{p} = p_i\) kaikilla \(i \in \{1, 2, \ldots, n\}\) voidaan kuitenkin pitää korkeintaan epärealistisena työskentelyoletuksena.
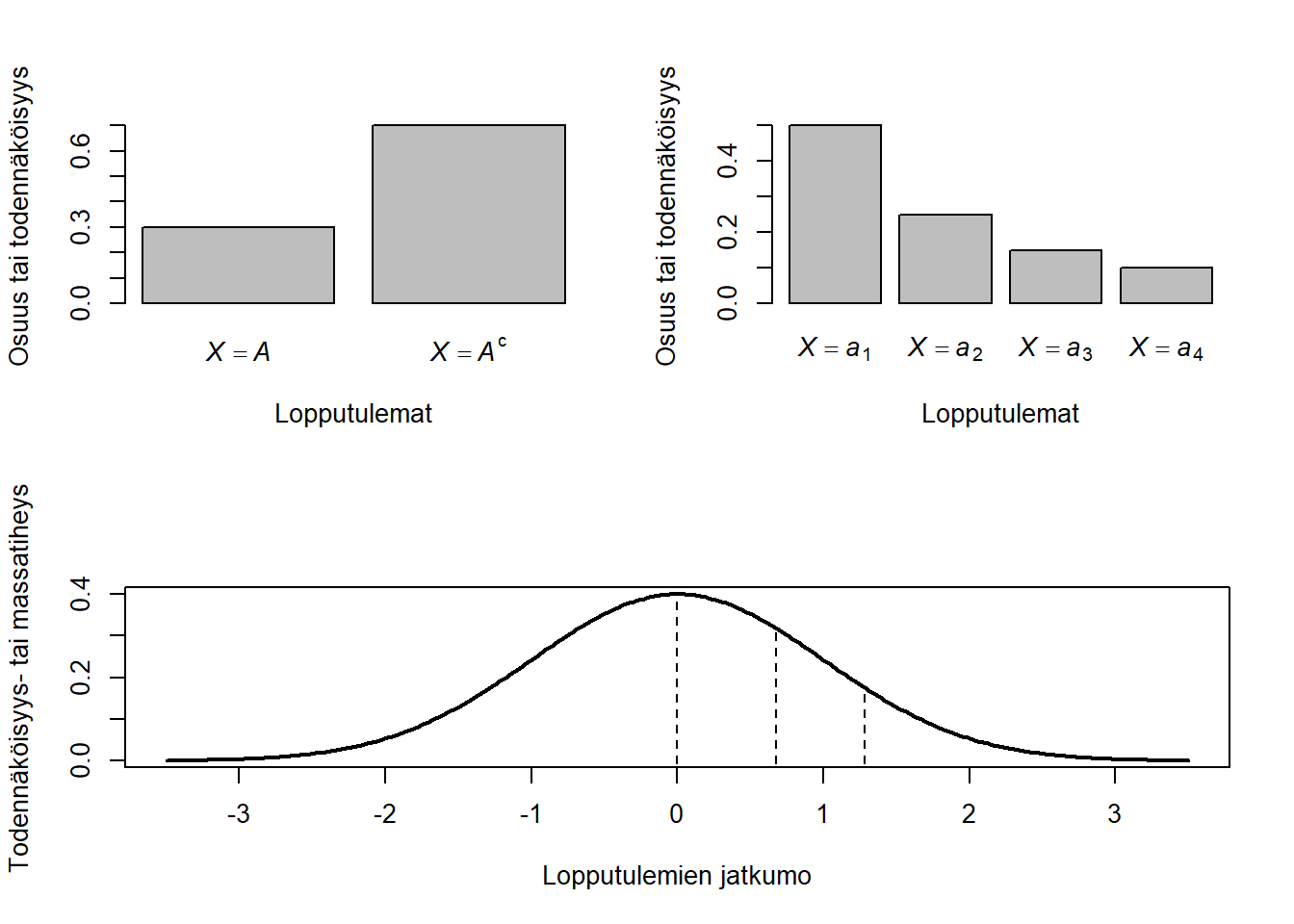
Empiirisessä tarkastelussa kahden mahdollisen lopputuleman (binäärisen) muuttujan jakauma esitetään usein alla olevan kuvan ylävasemman paneelin tapaan. Usein on mielenkiintoista sallia useampia kuin kaksi vaihtoehtoa samalle satunnaismuuttujalle. Esimerkiksi, työikäisten väestön ammattiasemaa voi olla mielekästä mallintaa vaihtoehdoin “töissä” ja “työtön”, mutta yleisemmin on sallittava mm. myös vaihtoehdot “opiskelija” ja “eläkeläinen”. Tällainen useamman tapahtuman diskreettiarvoinen jakauma saattaisi näyttää esimerkiksi ao. kuvan yläoikealta paneelilta. Ammattiasema-muuttujan mahdollisilla tapahtumilla \(\{a_1, a_2, a_3, a_4\}\), eli {töissä, työtön, opiskelija, eläkeläinen} ei ole ilmeistä luonnollista järjestystä – väite \(a_1 \le a_2\) on epälooginen. Tällaista muuttujaa kutsutaan nominaaliasteikolliseksi, tai lyhyesti nominaaliseksi. Kun taas voidaan ajatella pätevän \(a_i \le a_j\) kaikille \(i \le j\), muuttujaa kutsutaan ordinaaliasteikolliseksi, tai lyhyesti ordinaaliseksi. Saman näköisistä jakaumistaan huolimatta, ordinaaliasteikko rajaa mahdollisia todennäköisyysmalleja tuntuvasti nominaaliasteikkoa enemmän. Jokainen ordinaalinen tapahtuma \(a_i\) voidaan ilmaista muotoa \(\{Y \in (c_{i-}, c_{i}] \}\) olevina tapahtumina, missä \(Y\) on jokin jatkuva-arvoinen satunnaismuuttuja ja \(c_{i-1} < c_i\) ovat sen piileviä raja-arvoja (pystykatkoviivat ao. kuvan alimmassa paneelissa; Huom., \(c_0 = - \infty\) ja \(c_{\max(i)} = \infty\)). Alla oleva paksu yhtenäinen viiva kuvaa tiheysfunktiota, joka kertoo millä arvoalueella jatkuarvoisen satunnaismuuttujan todennäköisimmät arvot sijaitsevat (tai suurin osuus empiirisen jakauman yksiköistä). Ordinaalimuuttuja on siis olennaisesti yhdistelmäkuvaus, jossa \(Y\) kuvaa alkeistapahtuman reaaliluvuille ja \(X\) edelleen reaaliluvun diskreettiin joukkoon (esim. \(\{a_1, a_2, a_3, a_4\}\)). Alkuperäisen todennäköisyysavaruuden avulla ilmaistuna tapahtuman \(\{X = a_1\}\) todennäköisyys on tällöin muotoa \(P(X = a_1) = P(\{\omega \in \Omega : X(Y(\omega)) = a_1\})\), eli niiden alkeistapahtumien joukko, joka kuvautuu siihen reaalilukuväliin, joka kuvautuu arvoksi \(a_1\).

Likert-asteikolliset kyselyiden kysymykset ovat esimerkki ordinaalisesta muuttujasta. Ajatellaan, että on vaikea sanoa onko henkilöllä ollut uniongelmaa, kun viimeisen kahden viikon aikana hän on nukkunut osan öistä hyvin ja osan huonosti. Tällöin saatetaan ottaa käyttöön samankaltainen ratkaisu kuin on tehty yhdessä käytetyimmistä masennusoirekyselyistä: PHQ-9-mittari kysyy vastaajaltaan onko hän kahden viimeisen viikon aikana kokenut nukahtamis- tai nukkumisvaikeuksia tai liiallista nukkumista (\(a_1\)) “ei lainkaan”, (\(a_2\)) “useina päivinä”, (\(a_3\)) “useammin kuin puolet ajasta” vai (\(a_4\)) “lähes joka päivä”. Tässä tapauksessa yllä oleva formaali väliintuleva satunnaismuuttuja \(Y\) edustaa likimain tarkkaa kumulatiivista aikaa ja esim. tapahtuma \(\{X = a_3\}\) kaikkia sellaisia aikakertymiä, joina henkilö on kokenut uniongelmia vähintään viikon (kahdesta viimeisimmästä), muttei kuitenkaan lähes joka päivä. Alkeistapahtumien perusjoukoksi taas voidaan ajatella ne maailmantilat, jotka vaikuttavat henkilöiden kahden edeltävän viikon uniongelmiin. PHQ-9 mittari käsittelee tällaisia oiremuuttujia antamalla niiden diskreeteille tapahtumille melko mielivaltaiset lukuarvot (\(\{X = a_1\} \mapsto 0\), \(\{X = a_2\} \mapsto 1\), \(\{X = a_3\} \mapsto 2\) ja \(\{X = a_4\} \mapsto 3\)) ja laskemalla ko. pisteluvut yhteen yli oireiden (ns. summapiste). Myöhemmin kurssimateriaalissa näemme, että muunkinlainen ratkaisu olisi mahdollinen ja perusteltavissa.
Todennäköisyyden mittafunktion ominaisuuksista (Equation 2.1) seuraa tiettyjä rajoitteita jakaumille. Esimerkiksi, kaksiluokkaisen jakauman todennäköisyystiheyden ilmaisemiseen riittää yksi parametri \(p\), sillä komplementtiluokan todennäköisyyden on tällöin oltava \(q = 1 - p\), jotta \(p + q = 1\). Vastaavasti \(k\):n lopputuleman diskreetille jakaumalle pätevät todennäköisyydet \(\{p_1, p_2, \ldots, p_{k-1}, 1 - \sum_{k=1}^{k-1}\}\) ja jatkuvan jakauman tiheysfunktion \(f\) on täytettävä ehto \(\int f = 1\), eli x-akselin ja todennäisyysjakauman rajaaman alueen on oltava pinta-alaltaan yksi.
3.2 Jakauman määritelmä ja ominaisuuksia
Abstraktissa ja yleisimmässä käsittelyssä todennäköisyysjakauma on mitta. Edellisessä kappaleessa näimmekin kuinka todennäköisyysarvot “mittasivat” tapahtuvan toteuttavien alkeistapahtumien suhteellista osuutta perusjoukossa. Mittateoria on kuitenkin melko abstraktia ja monessa sovelluksessa sen erityistapaukset, integraali ja summa, riittävät mainiosti. Kun satunnaismuuttuja \(X\) noudattaa diskreettiä jakaumaa, todennäköisyys sen arvojoukolle \(A\) on
\[ P(X \in A) = \sum_{x \in A} P(X = x), \] missä pikkukirjain \(x\) on satunnaismuuttujan toteutunut arvo ja iso \(X\) itse muuttuja, ja summa on yli kaikkien joukkoon \(A\) kuuluvien arvojen. Jos joukko \(A\) on muotoa \(\{X \le a\}\), puhutaan kumulatiivisesta jakaumasta ja merkitään
\[ F(a) = \sum_{x \le a} P(X = x). \] Esimerkiksi ammattiasema-muuttujan kohdalla \(p_1 = P(X = a_1)\) jne. Kun \(X\) voi saada jatkuarvoisesti mielivaltaisen lähellä toisiaan olevia järjestettyjä lukuarvoja, ei tyypillisesti ole mielekästä edes kysyä yhden tietyn luvun todennäköisyyttä. Sen on oltava nolla. Nimittäin lukua \(a\) pienempiä reaalilukuja on äärettömästi ja jos äärettömän moni \(x \le a\) saisi nollaa suuremman todennäköisyyden yllä oleva summa olisi ääretön ja suurempi kuin yksi, tarkoittaen ettei \(P\) olisi todennäköisyys (Equation 2.1). Ongelma ratkaistaan esittelemällä todennäköisyystiheyden käsite, jolloin ylläoleva summa muuttuu integraaliksi. Yhtä hyvin voisi myös ajatella diskreetin todennäköisyyden perustuvan tiheysfunktioon \(f\) siten, että \(P(X = a_i) = \int_{a_{i-1}}^{a_i} f(x)dx\), jolloin yllä oleva summa muuttuu muotoon
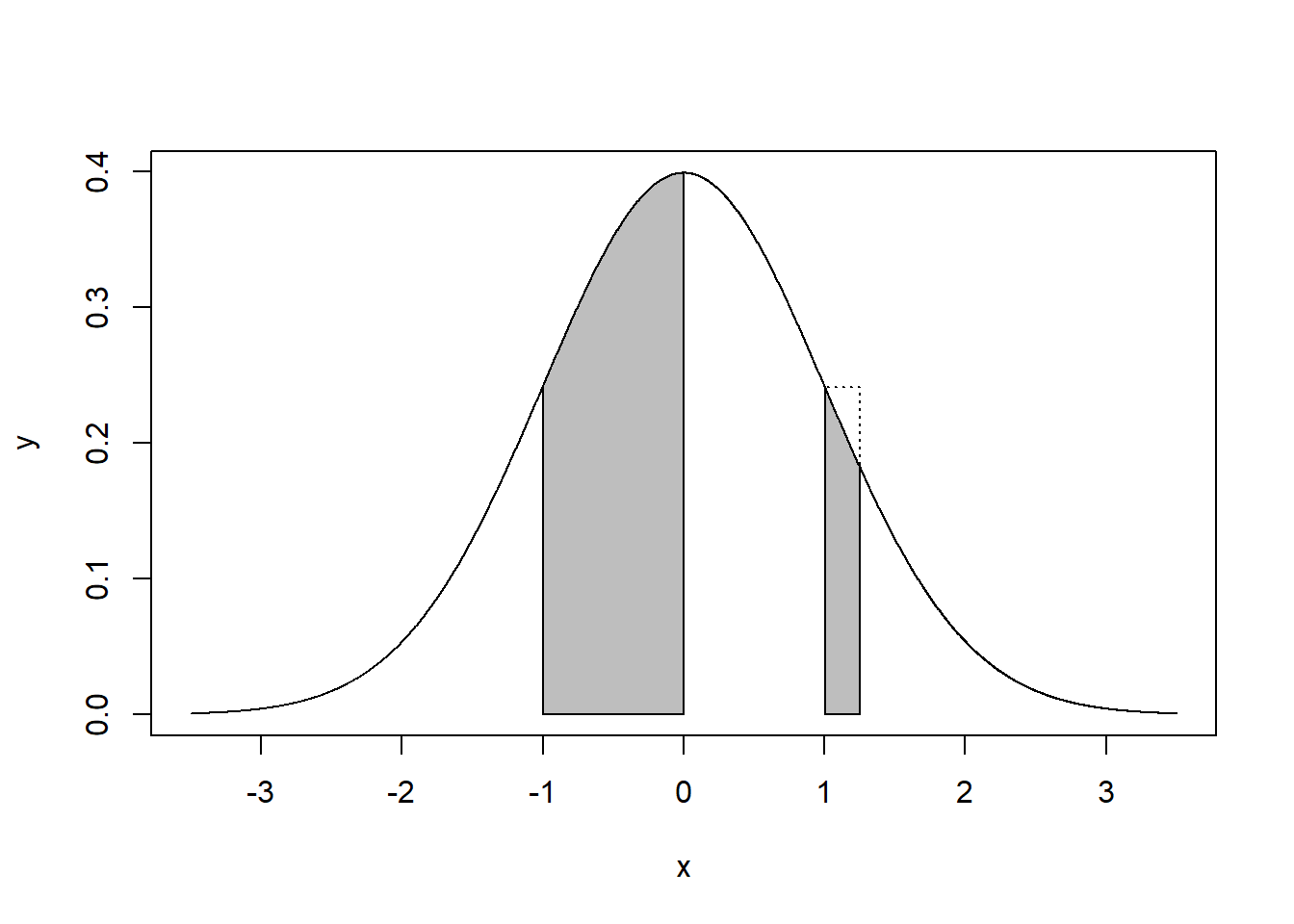
\[ F(a) = \int_{x \le a} f(x) dx. \] Todennäköisyys on siis mittaintegraali yli jonkin joukon ja kumulatiivinen todennäköisyysjakauma \(F(a)\) on mittaintegraali yli joukon \(\{-\infty, a\}\). Esimerkiksi, jos \(f\) on alla kuvatun jatkuva-arvoisen “normaalijakauman” tiheysfunktio, \(X\) on normaalijakautunut ja kysymme todennäköisyyttä sille, että se saa arvon, joka on joko miinus yhden ja nollan tai ykkösen ja kakkosen välissä (\(P(X \in [-1, 0] \cup [1, \frac{5}{4}]) = P(-1 \le X \le 0) + P(1 \le X \le \frac{5}{4})\)), tällöin tuota todennäköisyyttä vastaa kuvassa Figure 3.2 harmaaksi värjätty pinta-ala. Huomaamme myös, että todennäköisyysmitta yli pienen alueen on hyvin lähellä lukua tiheysfunktio \(\times\) alue, eli \(P(1 \le X \le \frac{5}{4}) \approx f(1) \times (\frac{5}{4} - 1) = f(1)\frac{1}{4}\) (tarkka integroitu pinta-ala eroaa vain katkoviivan rajaaman aluen verran karkeasta neliskulmiolla arvioidusta alasta). Tavallinen integraali voidaan määritellä tällaisten pienten vierekkäisten palkkien summana, kun palkeista tehdään yhä kapeampi x-akselin suunnassa, kuitenkin koko alue niillä täyttäen (palaamme määritelmään seuraavassa luvussa).
Oikeastaan todennäköisyyden ominaisuudet määrittyvät täysin jo aksioomista Equation 2.1. Niiden vuoksi yllä määritellylle kumulatiiviselle jakaumalle pätee, että \(F\) on ei-vähenevä funktio ja \(0 \le F(x) \le 1\) kaikilla \(x\). Myös \(\lim_{x \to -\infty} F(x) = 0\), \(\lim_{x \to \infty} F(x) = 1\) ja \(P(a \le X \le b) = F(b) - F(a)\). Vastaavasti, mikä hyvänsä yo. ominaisuudet täyttävä funktio \(F\) on jonkin todennäköisyysjakauman kumulatiivinen todennäköisyysjakauma. Kumulatiivinen todennäköisyysjakauma (kertymäfunktio) on hyödyllinen tapahtumien todennäköisyyksiin liittyvissä käytännön laskuissa. Odotusarvoissa taas tarvitaan todennäköisyysjakaumaa, eli tiheysfunktiota.
3.3 Odotusarvo
Odotusarvo ja varianssi-kovarianssi ovat paitsi keskeisiä jakaumien tunnuslukuja myös sovelluksissa tärkeitä aineistokuvauksia. Esimerkiksi, rakenneyhtälömallit usein perustuvat yksinomaan keskiarvon ja havaittujen korrelaatioiden mallintamiseen teoreettisesti johdettujen odotusarvojen ja kovarianssien avulla. Rakenneyhtälöiden erityistapauksia taas ovat mm. faktorianalyysi ja viiden suuren persoonallisuuspiirteen teoria. Kun \(X\) on reaalilukuarvoinen todennäköisyysavaruudessa \((\Omega, \mathcal{F}, P)\) määritelty satunnaismuuttuja ja \(P\):llä on tiheysfunktio \(f\), odotusarvon määritelmä on
\[ \begin{aligned} \text{E}[X] & = \int_{\Omega} X dP \\ & = \int_{\mathbb{R}} x f(x) dx, \end{aligned} \]
missä ensimmäinen integraali on hyvin yleinen Lebesque-integraali ja toinen integraali tavallinen integraali. Tällä kurssilla emme opeta mittateoriaa Lebesque-integraalin ymmärtämiseksi, mutta on hyvä tiedostaa myös tämä tavallinen merkintätapa, jottei se häiritse käsitteellisen ymmärryksen muodostamista sovelluksista lukiessa. Tyypillisesti (muttei aina) kyse on samasta asiasta. Diskreetin muuttujan tapauksessa Lebesque-integraali palautuu summaksi siten, että \(\text{E}[X] = \sum_x xP(X = x)\). Esimerkiksi yhden nopan heiton odotusarvo on
\[ \begin{aligned} \text{E}[X_{\text{noppa}}] &= \sum_{x=1}^6 x P(X_{\text{noppa}} = x) \\ & = \sum_{x=1}^6 x \frac{1}{6} \\ & = 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6} \\ & = \frac{1}{6} \times (1+2+3+4+5+6) \\ & = \frac{21}{6} \\ & = 3 \frac{1}{2}. \end{aligned} \]
Tässä \(P(X_{\text{noppa}} = x)\) oli siis sama arvo kaikilla \(x\) yhdestä kuuteen, mutta näin ei tietysti aina ole. Esimerkiksi kahden nopan summan tapauksessa \(P(X_{\text{noppa 1}} + X_{\text{noppa 2}} = 2) = \frac{1}{36}\), mutta \(P(X_{\text{noppa 1}} + X_{\text{noppa 2}} = 7) = \frac{6}{36} = \frac{1}{6}\), kuten edellisessä luvussa näimme. Silti, kun asetetaan \(Y = X_{\text{noppa 1}} + X_{\text{noppa 2}}\), niin pätee, \(\text{E}[Y] = \sum_{y=1}^{12} yP(Y = y) = 7 = 3 \frac{1}{2} + 3 \frac{1}{2} = \text{E}[X_{\text{noppa 1}}] + \text{E}[X_{\text{noppa 2}}]\). Tämä ei ole sattuma, vaan odotusarvon yleisten ominaisuuksien seuraus. Odotusarvo on lineaarinen operaatio, eli:
\[ \begin{aligned} \text{E}[X + Y] &= \text{E}[X] + \text{E}[Y] \text{ satunnaismuuttujille } X, Y \\ \text{E}[cX] &= c \text{E}[X] \text{ vakiolle } c. \\ \end{aligned} \] Osoitamme tämän yleisen totuuden kahden (mahdollisesti toisistaan riippuvan) nopan heiton erityistapauksessa. Yleiset todeistukset menevät pitkälti samoin, mutta diskreetti tapaus välttää integraalilaskennan. Notaation helpottamiseksi ja yleistä tapausta lähestyäksemme, merkitään \(X = X_{\text{noppa 1}}\) ja \(Y = X_{\text{noppa 2}}\). Kun muistamme edellisen kappaleen ehdollisen ja kokonaistodennäköisyyden kaavat, näemme, että
\[ \begin{aligned} \text{E}[X + Y] &= \sum_{x=1}^6 \sum_{y=1}^6 (x + y) P(X = x, Y = y) \\ &= \sum_{x=1}^6 \sum_{y=1}^6 x P(X = x, Y = y) + \sum_{x=1}^6 \sum_{y=1}^6 y P(X = x, Y = y) \\ &= \sum_{x=1}^6 x \sum_{y=1}^6 P(X = x,|Y = y)P(Y = y) + \sum_{y=1}^6 y \sum_{x=1}^6 P(Y = y|X = x)P(X = x) \\ &= \sum_{x=1}^6 x P(X = x) + \sum_{y=1}^6 y P(Y = y) \\ &= \text{E}[X] + \text{E}[Y] \end{aligned} \] Mieti miksi myös vakion saa ottaa odotusarvon eteen. Varianssi ja kovarianssi ovat vaihtelun ja yhteisvaihtelun määrää mittaavia tunnuslukuja ja nekin määritellään odotusarvon avulla seuraavasti:
\[ \begin{aligned} \text{Var}[X] &= \text{E}\big[(X - \text{E}[X])^2 \big], \\ \text{Cov}[X, Y] &= \text{E}\big[(X - \text{E}[X])(Y - \text{E}[Y]) \big]. \end{aligned} \]
Satunnaismuuttujien muunnokset ovat nekin satunnaismuuttujia. Koska laskettu odotusarvo \(\text{E}[X]\) on vain luku, poikkeama keskiarvosta, \((X - \text{E}[X])^2\), on siis satunnaismuuttujan \(X\) algebrallinen muunnos. Varianssi on tällaisen muunnosmuuttujan odotusarvo, eli odotusarvo poikkeamalle odotusarvosta. Keskihajonta määritellään \(\sqrt{\text{Var}[X]}\) ja kuvastaa vaihtelua muuttujan alkuperäisessä yksikössä, varianssin yksikön ollessa alkuperäisen neliö. Korrelaatio määritellään \(\frac{\text{Cov}[X, Y]}{\sqrt{\text{Var}[X]} \sqrt{\text{Var}[Y]}}\). Odotusarvo ja varianssi voidaan määritellä myös ehdollisena jollekin tapahtumalle \(B\), jolloin
\[ \begin{aligned} \text{E}[X|B] &= \sum_x x P(X = x|B), \\ \text{Var}[X|B] &= \text{E}\big[(X - \text{E}[X|B])^2|B \big]. \end{aligned} \]
Tässä \(\text{E}[X|B]\) saa siis eri arvot sen mukaan sattuuko \(B\) vai ei. Toisin kuin tavallinen odotusarvo, ehdollinen odotusarvo on siis satunnaismuuttuja, eikä yksittäinen luku. Se on luku vain, kun tapahtuma \(B\) on jo sattunut (tai ajatellaan tapahtuneeksi). Jokseenkin hämäävästi, \(\text{E}[X|Y]\) on siis muuttujan \(Y\) funktio. Ehdolliselle odotusarvolle pätee tärkeä kokonaisodotusarvon laki:
\[ \begin{aligned} \text{E}\big[\text{E}[X|Y] \big] &= \text{E}\big[ \sum_x x P(X = x|Y) \big] \\ &= \sum_y \big\{ \sum_x x P(X = x|Y = y) \big\} P(Y = y) \\ &= \sum_x x \sum_y P(X = x|Y = y) P(Y = y) \\ &= \sum_x x P(X = x) \\ &= \text{E}[X]. \end{aligned} \]
Seuraavassa kappaleessa tarvitsemme erityisesti kokonaisodotusarvon erityistapausta, \(\text{E}[X] = P(B)\text{E}[X|B] + P(B^c)\text{E}[X|B^c]\).
3.4 Tärkeitä jakaumia
Tyypillisesti jakaumia kuvataan tiheys- tai todennäköisyysfunktionsa kautta, vaikka toisinaan myös yo. tunnuslukuja ja muita yleisiä ominaisuuksia koskevat rajoitteet riittävät jakauman yksikäsitteiseen määrittelyyn. Annamme tässä jatkoa varten muutaman todennäköisyys- ja tiheysfunktioon perustuvan määritelmän ja havainnollistavan kuvan.
3.4.1 Binääriset jakaumat
3.4.1.1 Bernoulli-jakauma
Kaksiluokkaisen ns. Bernoulli-tapahtuman todennäköisyydet ovat \(P(X = x) = p\) ja komplementtitapahtumalla pakosti siis \(P(X = x^c) = 1 - p\). Tässä yhteydessä on tavanomaista merkitä tapahtumaa \(x\) luvulla 1 (esim. “yksi onnistuminen”) ja tapahtumaa \(x^c\) luvulla 0 (esim. “ei onnistumista”). Parametri \(p\) (onnistumistodennäköisyys) siis määrittelee Bernoulli-jakauman.
3.4.1.2 Binomijakauma
Tällaisten riippumattomien tapahtumien sarjan \(\{X_1, X_2, \ldots, X_n \}\) todennäköisyys on tällöin \(P(X_1, X_2, \ldots, X_n) = \prod_{i=1}^n P(X_i) = p^{\sum x_i} (1 - p)^{n - \sum x_i}\). Tämä on kuitenkin todennäköisyys juuri kyseisessä järjestyksessä saadulle ykkös- ja nollatapahtumien jonolle ja määrittelee siis vain Bernoulli-tapahtumien jonon jakauman. Usein kuitenkin ollaan kiinnostuneita onnistumisten lukumäärästä ennemin kuin tarkasta järjestyksestä, eli siis summasta \(S = \sum_{i=1}^n x_i\). Binomiaalisen jakauman klassinen sovellusesimerkki on ajatella sitä kruunien lukumäärän jakaumana \(n\):n lantin heiton sarjassa. Alakohtaisempi esimerkki voisi olla geneettisten riskialleelien lukumäärä \(n\):n yhden emäksen polymorfismin (engl. single-nucleotide polymorphism, eli SNP, tuttavallisemmin “snippi”) alleelien joukossa, joista jokainen \(X_i\) saa joko arvon \(X_i = 1\), eli riski, tai \(X_i = 0\) (ei riskiä). Jos geneettiset riskit ovat ns. additiivisia, \(S\) edustaa geneettistä kokonaisriskiä. Jos nyt hieman epärealistisesti oletamme, että riskialleelin yleisyys on jokaisella snipillä tasan \(p = \frac{1}{2}\), jolloin myös \((1 - p) = \frac{1}{2}\), voimme todeta \(P(X_1, X_2, \ldots, X_n) = (\frac{1}{2})^{\sum x_i} (\frac{1}{2})^{n - \sum x_i} = \frac{1}{2^n}\). Koska todennäköisyydet ovat symmetrisiä ja jokainen jono yhtä todennäköinen, todennäköisyyden aksioomista (Equation 2.1) seuraa, että \(\sum_{\{\text{erilliset tulosjonot}\}} \times \frac{1}{2^n} = 1\), eli erillisiä tulosjonoja on \(2^n\) kappaletta. Erillisiä riskipiste summia on vain \(n+1\) kappaletta.
Kuten edellisen luvun kahden nopan heiton esimerkissä, on huomioitava, että tiettyjä summa-arvoja saadaan todennäköisemmin kuin toisia. Esimerkiksi tapauksessa \(n = 2\), summan \(S = 1\) tuottavat tulosjonot \(\{X_1 = 1, X_2 = 0\}\) sekä \(\{X_1 = 0, X_2 = 1\}\), joten \(P(S = 1) = \frac{1}{2^n} + \frac{1}{2^n} = \frac{2}{4} = \frac{1}{2}\). Sen sijaan, summa \(S = 2\) saavutetaan vain ja ainoastaan tulosjonolla \(\{X_1 = 1, X_2 = 1\}\), eli \(P(S = 1) = \frac{1}{4}\). Järkeilyä voidaan yleistää suuremmille \(n\) huomaamalla, että kukin toteutunut tapahtuma vastaa osajoukkoa \(\{x_i: x_i = 1\} \subset \{x_1, x_2, \ldots, x_n \}\). Joukkoa \(\{x_i: x_i = 1\}\), jossa on k alkiota, kutsutaan k-variaatioksi. On olemassa \((n)_k = n(n-1)(n-2) \cdots (n - k + 1)\) mahdollista k-variaatiota tapahtumasta, jossa \(k\) kpl satunnaismuuttujista \(\{X_1, X_2, \ldots, X_n \}\) saa arvon yksi ja loput nollan (eli \(S = k\)). Ensimmäinen ykkönen voidaan sijoittaa mihin vain muuttujista, jolloin toiseksi voidaan valita mikä vain jäljelle jäävistä \(n - 1\) muuttujasta, jne. Variaatiot ovat edelleen järjestettyjä jonoja (indeksin suuruuden mukaan). k-variaation järjestyksiä (permutaatioita) on \(k! = k(k-1)(k-2) \cdots 1\) kpl. Näin ollen k:n ykkösen kombinaatioita, eli järjestämättömiä joukkoja, on oltava yhteensä
\[ \begin{aligned} \frac{(n_k)}{k!} &= \frac{n(n-1)(n-2) \cdots (n - k + 1)}{k!} \\ & = \frac{n(n-1)(n-2) \cdots (n - k + 1)}{k!} \times \frac{(n-k)!}{(n-k)!} \\ & = \frac{n!}{k!(n-k)!} \\ & =: \binom{n}{k}. \end{aligned} \]
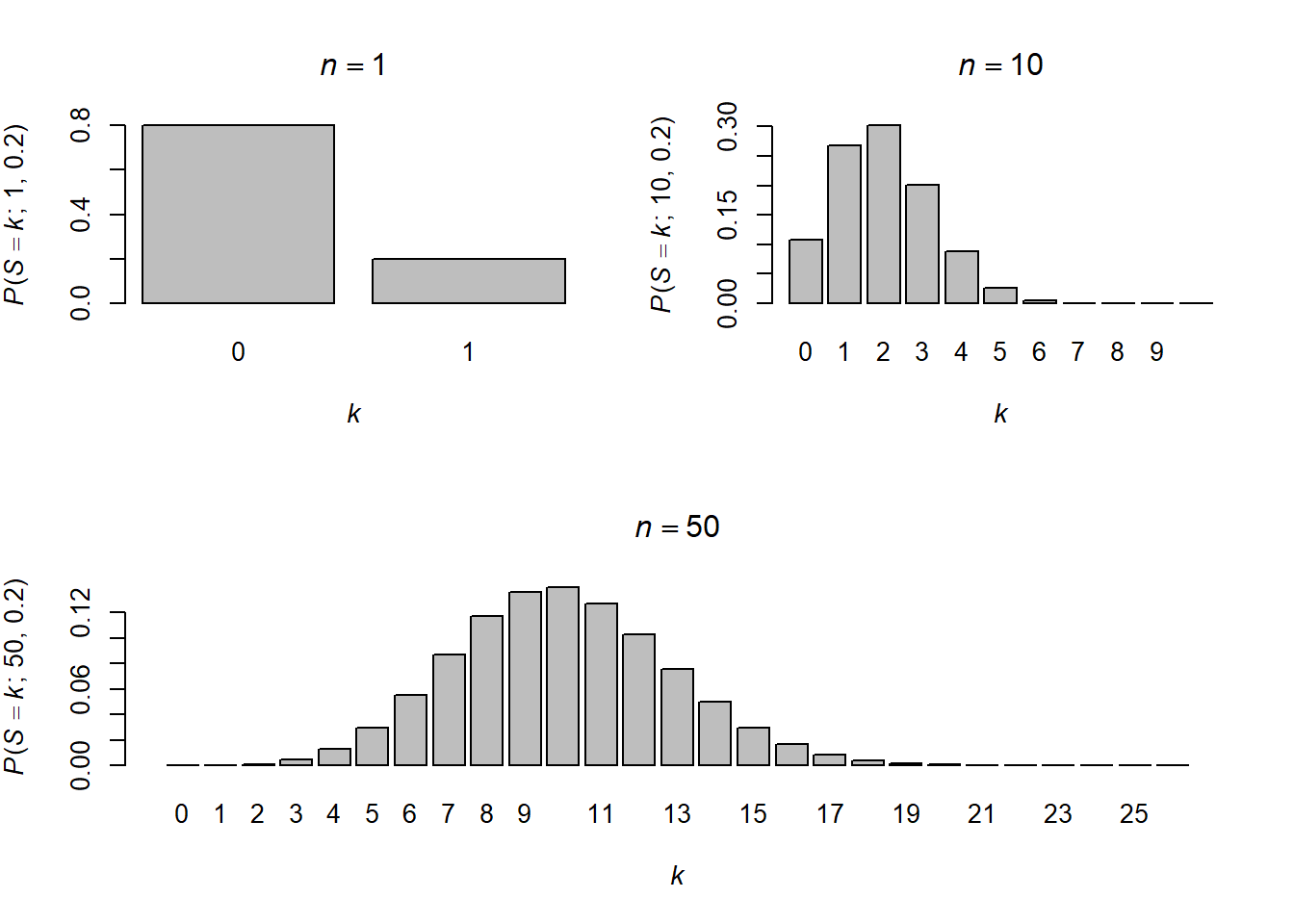
Kutsumme tässä (symbolilla \(=:\)) määriteltyä lukua \(\binom{n}{k}\) binomikertoimeksi. Binomijakaumaksi, eli summan \(S\) todennäköisyydeksi, saadaan parametreilla \(n\) riippumatonta muuttujaa (lantin heittoa, riskialleelia, tmv.) ja tapahtumatodennäköisyys \(p\) (kruunan, riskialleelin, tmv.) \[ P(S = k; n, p) = \binom{n}{k} p^{k} (1 - p)^{n - k} \] Alla oleva kuva antaa muutaman esimerkin binomijakaumasta, joista ensimmäinen esimerkki palautuu Bernoulli-jakaumaan.
3.4.1.3 Normaalijakauma
Aiemman luvun kuvasta (Figure 2.4) näimme kuinka kahden nopan heiton summan jakauma on yksihuippuinen, vaikka itse noppien silmälukujen jakauma on tasainen (antaen todennäköisyyden 1/6 kaikille silmäluvuille). Muoto ei ole sattumaa. Alkuperäisestä jakaumasta riippumatta, satunnaismuuttujien summat lähestyvät tiettyä yksihuippuista jakaumaa summatermien lisääntyessä. Alla oleva kuva havainnollistaa tilannetta binomijakauman tapauksessa, joka siis on Bernoulli-jakautuneiden satunnaismuuttujien summan jakauma. Kun otoskoko kasvaa 50:n yksikköön (eli satunnaismuuttujaan), niin todennäköisyydet saada nolla “onnistumista” tai tietty 25:n ylittävä määrä ovat häviävän pieniä (\(< 0.00001\) ja \(< 0.0000001\)), kun taas odotusarvolukumäärä \(0.2 \times 50 = 10\) saadaan edelleen verrattain suurella todennäköisyydellä (~0.14). Todennäköisyydet siis keskittyvät odotusarvon ympärille ja tämä havainto on tilastotieteessä erittäin keskeinen. Sitä käsitelläänkin seuraavassa luvussa keskeiseksi raja-arvolauseeksi kutsutun teoreettisen tuloksen kohdalla.
Normaalijakauma eli Gaussin jakauma on se todennäköisyysjakauma, jota satunnaismuuttujien keskiarvot, otoskoolla vakioidut summat, lähestyvät summatermien lisääntyessä. Yllä olevasta Binomijakauman käsittelystä näemme kuinka “häntätodennäköisyydet” tapahtumille \(S = 0\) ja \(S = n\) laskevat eksponentiaalisesti, kun \(n\) kasvaa, eli \(P(S = 0; n, \frac{1}{2}) = \frac{1}{2^n} = 2^{-n} = \frac{1}{2^{n}}\). Eksponenttifunktio kertoo tiettyä kantalukua, joka edellä on siis \(2\). Eli seuraavat merkinnät vastaavat siis toisiaan: \(2^n = \prod_{i=1}^n 2 = 2 \times 2 \times \cdots \times 2\). Huomionarvoista tässä on, että eksponenttifunktio muuttaa summat kertolaskuiksi, eli \(2^{2+3} = 2^2 \times 2^3\), lyhyemmin \(2^2 2^3\). Erinäisistä matemaattisista syistä, lukua ~2.718 kutsutaan eksponenttifunktion luonnolliseksi kannaksi ja merkitään \(e\). Eksponenttifunktion käänteisfunktio on logaritmi: \(x = \log(e^x) = e^{\log(x)}\) kaikilla \(x\). Logaritmi siis muuttaa kertolaskut summiksi, ja näin ollen, kaikki eksponenttifunktiot voidaan kirjoittaa luonnollisessa kannassa jollain kasvuvauhdilla, esim. \(2^n = e^{\log2^n} = e^{n \log2} = e^{\alpha n}\), missä siis kasvuvauhti on \(\alpha = \log2\) (arvoilla \(\alpha < 0\) funktio on vähenevä). Toinen saman eksponenttifunktion yleinen merkintätapa on \(\exp(\alpha n)\), eli \(e = \exp(1)\). Eksponenttifunktio on hyvin nopeasti laskeva tai vähenevä funktio, joka esiintyy myös Normaalijakauman määritelmässä. Normaalijakauma määritellään tiheysfunktionsa kautta, joka riippuu odotusarvoparametrista \(\mu\) sekä keskihajontaparametrista \(\sigma\) ja on muotoa
\[ f(x;\mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} . \]
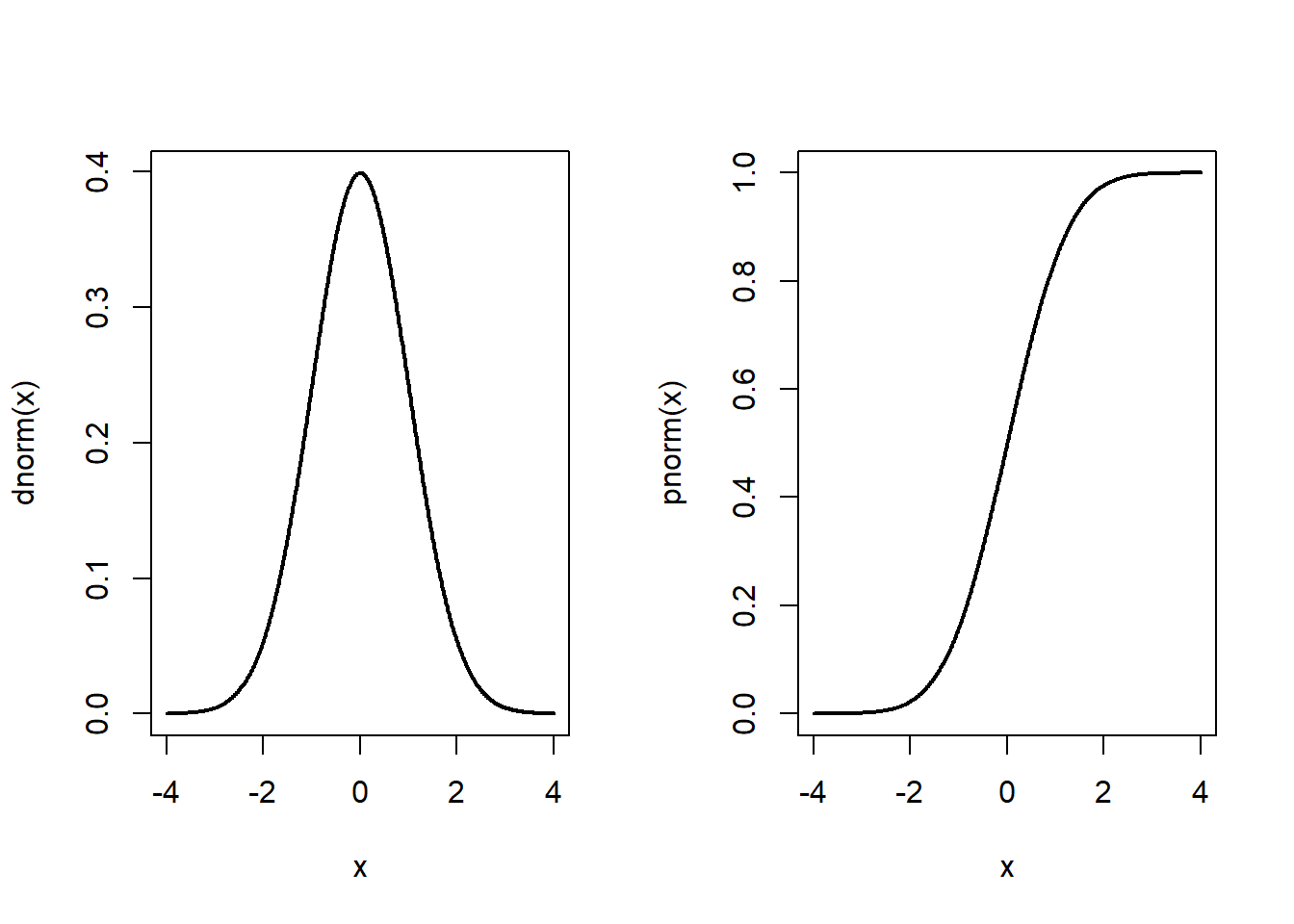
Ns. standardinormaalijakauma saadaan tästä asettamalla \(\mu = 0\) ja \(\sigma = 1\). Sitä, että satunnaismuuttuja on normaalisti jakautunut merkitään usein lyhyesti: \(X \sim N(\mu, \sigma)\). Jos satunnaismuuttuja \(Z\) on standardinormaalijakautunut, \(Z \sim N(0, 1)\), niin tiedetään, että \(\mu + \sigma Z \sim N(\mu, \sigma)\). Vastaavasti, \((X - \mu)/\sigma ~\sim N(0, 1)\). Teoreettisten tulosten kannalta riittää siis usein tutkia standardinormaalijakaumaa. Alla olevassa kuvassa näemme standardinormaalijakauman tiheysfunktion (vasemmalla) sekä kertymäfunktion (oikealla). Todennäköisyyksien kannalta standardinormaalijakauman yksiköitä voidaan ajatella minkä tahansa normaalijakautuneen muuttujan keskihajontoina. Esimerkiksi, todennäköisyys, että normaalisti jakautunut satunnaismuutta \(X\) saa yhden tai useamman keskihajonnan verran odotusarvoaan pienemmän arvon on \(\int_{-\infty}^{-1} f(x;0,1)dx \approx 0.16\). Odotusarvon alittaminen tai ylittäminen yli kahdella keskihajonnalla on jo hyvin epätodennäköistä, molemmat tismallaan yhtä epätodennäköistä (\(\int_{-\infty}^{-2} f(x;0,1)dx = \int_{2}^{\infty} f(x;0,1)dx \approx 0.02\)). Normaalijakauma on siis symmetrinen odotusarvonsa ympärillä.
3.4.1.3.1 Normaalijakauman käyttöesimerkkejä
Koska mittausvirheet usein johtuvat usean riippumattoman tekijän summasta, normaalijakaumaa on pidetty hyvänä virhejakaumana. Tässä tarkoituksessa Carl Friedrich Gauss sen myös vuonna 1823 johti teoreettisesti. Fysiikassa diffusoivan partikkelin lokaatio jakautuu normaalisti. Tässäkin on taustalla partikkeliin törmäävät useat muut molekyylit. Einstein käyttikin tätä teoreettista mallia ja diffuusioprosessia koskevia havaintoja atomin olemassa olon todistelussa. Psykologian parissa erityisesti Luis Leon Thurstone (1887-1955) alkoi käyttämään normaalijakaumaa älykkyysosamäärän jakaumana. Yksilön älykkyyshän saattaisi hyvinkin olla usean riippumattoman tekijän summa (geenit, ravinto, ympäristöaltistukset, jne). Myös psykopatologian taustalla vaikuttavan riskin on ajateltu jakautuvan normaalisti väestössä. Erityisesti tätä mallia on käytetty geneettisen riskin kuvauksena, koska siihan vaikuttavat useat toisistaan riippumattomat geenipolymorfismit (Plomin et al. 2012). Normaalijakauma on siis paljon käytetty malli usealla tieteenalalla. Tärkein tämä malli lienee silti Tilastotieteelle. Tilastotieteen kannalta tärkeitä käyttöesimerkkejä käsitelläänkin kattavammin luvussa 5.
Normaalijakauman teoreettinen merkitys on myös kenties tehnyt siitä liian suositun monella alalla. Esimerkiksi masennusoireilun taustalla vaikuttava riski ei empiiristen aineistojen valossa näyttäisi kuitenkaan olevan normaalisti jakautunut, vaikka oireisiin lukuisat geenit vaikuttavatkin (Talkkari and Rosenström 2024). Kukaan ei myöskään osaa varmaksi sanoa voiko ihmisen älykkyyden vangita yhteen skalaariparametriin, saati suoraan millään instrumentilla havainnoinut sellaisen parametrin jakautumista väestössä. Normaalijakaumaan perustuvat mallit ovat hyödyllisiä tieteissä, mutta eivät saman arvoisia kaikissa tieteissä. Kokeneemmillekin tutkijoille on toisinaan tullut yllätyksenä, etteivät usean riippumattoman tekijän funktiona muodostuvat ilmiöt jakaudu normaalisti - ainoastaan summat. Arkikielessähän herkästi sanomme vaikka, että “koettu stressi on usean tekijän summa”, kuitenkaan tarkoittamatta juuri tarkalleen summaa. Puhuja ei välttämättä fraasillaan sulje pois mahdollisuutta, että stressi onkin ennemmin tulo: “yksi ikävä asia ei paljoa paina, mutta useammat kertautuvat”. Satunnaismuuttujien tulot eivät kuitenkaan jakaudu lainkaan normaalisti [ne jakautuvat Log-Normaalisti, eli hyvin vinosti]. Näemme siis, että arkikielessä hyvin samankaltaiset fraasit johtavat tarkemmassa tieteellisessä tarkastelussa hyvin erilaisiin malleihin. Tutkijan on tärkeää pitää tämä mielessään. Sen ymmärtäminen miksi ja miten normaalijakautunutta havaintoaineistoa muodostuu paitsi tukee ko. jakaumaan liittyvien työkalujen ja paremetrien käyttöä epäilemättä myös lisää mielenkiintoa muita työkaluja kohtaan.