2 Määritelmät
Tässä kappaleessa tutustumme todennäköisyyden määritelmään. Vaikkemme kurssin puitteissa voikaan tyhjentävästi esittää määritelmää sen edellyttämien matemaattisten taustatietojen vuoksi, voimme kuitenkin esimerkkien kautta luoda siitä hyvän alakohtaisen käsityksen. Tarkempi intuitio tukee tarkempaa ajattelua jatkossa, mikä on hyvä asia. Vaikka tyhjentävä esitys on usein älyllisesti tyydyttävä asia sekin, vanhan sanonnan mukaan täydellinen on hyvän pahin vihollinen. Tässä tapauksessa täydellinen edellyttäisi syventävän tason matematiikan opintoja, jotka edellyttävät esitietoina kandidaatin opinnot, joten tyydymme hyvään ja hyödylliseen - ainakin toistaiseksi. Etenemme esimerkkien kautta. Ensin kuitenkin esitämme matemaattisen mallin, johon tilastotiedekin pitkälti nojaa – todennäköisyysavaruuden. Matemaattisen mallin esitys nojaa paljon Pekka Tuomisen kirjaan (Tuominen 2004). Runsaasti lisää matemaattisia yksityiskohtia kiinnostuneille tarjoaa mm. Klenke (2008). Alun määritelmien jälkeen, käytämme enemmän myös alakohtaisia esimerkkejä. Todennäköisesti hyödyllinen lukustrategia on myöhemmän tekstin kohdalla toistuvasti palata tähän kappaleeseen, varmistaen, että on ymmärtänyt kuinka todennäköisyysavaruuden malli toimii kussakin sovelluksessaan. Abstraktit käsitteet muodostuvat omakohtaisiksi työkaluiksi vasta käytön myötä!
HUOM! Käytämme matemaattisessa käsittelyssä kansainvälisen käytännön mukaista desimaalipistettä, emme desimaalipilkkua. Tämä selkeyttää myös joukko-opillisia merkintöjä.
2.1 Todennäköisyysavaruus
Historiallisesti varhaisin todennäköisyysmalli perustuu symmetrisiin alkeistapahtumiin \(\omega_i\), jotka muodostavat perusjoukon \(\Omega = \{\omega_1, \omega_2, \omega_3, \ldots \}\). Perusjoukkoon viitataan usein myös otanta-avaruutena tai -joukkona ja alkeistapahtumiin satunnaiskokeen lopputulemina tai tuloksina. Alkeistapahtumat ovat siis perusjoukon alkioita. Esimerkiksi, nopan silmäluvut yhdestä kuuteen ovat symmetrisiä alkeistapahtumia, kun noppa on harhaton ja kaikki silmäluvut yhtä todennäköisiä.
Määritelmä. Tapahtuma \(A\) on perusjoukon \(\Omega\) jokin osajoukko.
Esimerkiksi, \(A = \{1, 2\}\) on tapahtuma, jos merkitsemme nopan silmälukuja perusjoukkona \(\Omega = \{1, 2, 3, 4, 5, 6\}\). Tapahtuma on sama, vaikka voimmekin sanallistaa sen eri tavoin, kuten “silmäluku on pienempi kuin 3” tai “noppa saa arvon 1 tai 2”. Jälkiviisauden valossa heitetty noppa toki sai vain yhden arvon (alkeistapahtuman), mutta todennäköisyyslaskennen tarkoitus on suhteuttaa toisiinsa erilaisia hypoteeseja (tapahtumia), jotka ennalta rajaavat sitä mitä saattaa tapahtua.
Kun on kyse symmetrisistä alkeistapahtumista, niiden todennäköisyys on luku
\[ P(A) = \frac{ \#(A)}{\#(\Omega)}, \]
eli tapahtuman \(A\) alkeistapahtumien lukumäärän suhde koko (symmetristen) alkeistapahtumien perusjoukon kokoon. Esimerkiksi, tapahtuman \(\{1, 2\}\) todennäköisyys on \(P(\{1, 2\}) = \frac{2}{6}\). Todennäköisyys saada juuri tietyt kaksi nopan silmälukua on kaksi kuudesta mahdollisesta silmäluvusta, eli \(\frac{2}{6}\), eli \(\frac{1}{3}\).
Yllä oleva numeerinen tulos ei toivottavasti yllätä tämän tekstin lukijaa, mutta olennaisempana asiana huomaamme, että todennäköisyysfunktion alkiot ovat joukkoja. Matematiikassa funktio kuvaa lähtöjoukon alkion maalijoukon alkioksi, mutta todennäköisyysfunktion kuvaama alkio (tapahtuma) on jo joukko (tarkemmin, perusjoukon osajoukko). Koska tapahtumat jo ovat joukkoja, tarkoittaa se, että todennäköisyysfunktion lähtöjoukon on oltava joukkojen joukko. Tätä joukkojen joukkoa kutsutaan tapahtuma-avaruudeksi.
Määritelmä. Tapahtuma-avaruus, eli \(\sigma\)-algebra, on kaikkien perusjoukon \(\Omega\) (olennaisten) osajoukkojen \(A \subset \Omega\) (tapahtumien) muodostama joukko \(\mathcal{F}\) (eli \(A\) on sen alkio, \(A \in \mathcal{F}\)).
Määritelmässä “olennaiset” osajoukot viittaavat lähinnä erityistapauksiin, joita esiintyy vain numeroimattomasti äärettömillä perusjoukoilla. Äärellisellä perusjoukolla, kuten nopanheiton mallissa, tapahtuma-avaruus tyypillisesti on perusjoukon kaikki osajoukot. Nopanheitossa mm. joukot \(\{2\}\), \(\{2, 5\}\) ja \(\{2, 3, 4\}\) ovat tapahtuma-avaruuden alkioita, vaikka \(\{2, 5\}\) ja \(\{2, 3, 4\}\) koostuvatkin heiton useasta mahdollisesta lopputulemasta. Myös tyhjä joukko, \(\emptyset\), sekä koko perusjoukko \(\Omega\) ovat aina tapahtuma-avaruuden alkioita, koska mielekkään \(\sigma\)-algebran on oltava suljettu tapahtumien komplementtien suhteen. Jos todennäköisyysmallissa halutaan todeta, että jokin nopan silmäluvuista saadaan varmuudella, \(P(\Omega)=1\), silloin on voitava todeta mahdottomaksi käänteistapahtuma “silmäluku on jokin muu kuin \(\Omega = \{1, 2, 3, 4, 5, 6\}\)”, eli \(P(\Omega^c)= P(\emptyset) = 0\), missä yläindeksi viittaa joukon komplementtiin (tapahtuman \(A \subset \Omega\) komplementti, eli vastatapahtuma, on \(\Omega \setminus A = A^c\), eli perusjoukon ja \(A\):n joukkoerotus). Noppaesimerkissä tapahtuman \(A = \{1, 2\}\) komplementti on \(A^c = \{3, 4, 5, 6\}\). Vaikka se nopanheiton kohdalla harvoin on mielekästä, tapahtuma-avaruudeksi voitaisiinkin periaatteessa määritellä vain joukot \(\mathcal{F} := \{\emptyset, \{1, 2\}, \{3, 4, 5, 6\},\{1, 2, 3, 4, 5, 6\}\}\). Se tarkoittaisi ettemme ole kiinnostuneita kaikista satunnaiskokeen (nopanheitto) alkeistapahtumista \(\omega\) vaan ainoastaan siitä, tapahtuuko “silmäluku on 2 tai alle”. Nopanheiton kohdalla on kuitenkin luontevaa määritellä tapahtuma-avaruus \(\mathcal{F}\) alkeistapahtumien perusjoukon \(\Omega\) kaikkien osajoukkojen kokoelmaksi. Toisin kuin nopanheiton kohdalla, aina (tai yleensä) ei ole teknisesti mahdollista määritellä tapahtuma-avaruutta kaikkien osajoukkojen kokoelmana. Siksi annetaan seuraava määritelmä, joka takaa tapahtumille kaikki (numeroituvat) joukko-operaatiot:
Tarkka (aksiomaattinen) määritelmä. Tapahtuma-avaruus, eli \(\sigma\)-algebra, on perusjoukon \(\Omega\) osajoukkojen kokoelma \(\mathcal{F}\), jolle pätee
\[ \begin{aligned} (1) & \hspace{3 cm} \Omega \in \mathcal{F} \\ (2) & \hspace{3 cm} A \in \mathcal{F} \Rightarrow A^c \in \mathcal{F} \\ (3) & \hspace{3 cm} A_i \in \mathcal{F} \ (i = 1, 2, \ldots ) \Rightarrow \bigcup_{i=1}^{\infty} A_i \in \mathcal{F} \end{aligned} \]
Tapahtuman todennäköisyys on funktio \(P\), joka kuvaa tapahtuma-avaruuden alkiot välin \([0, 1]\) alkioksi, eli ko. välin reaaliluvuiksi. Teknisesti merkitään \(P:\mathcal{F} \mapsto [0, 1]\). Funktiota kutsutaan usein myös “kuvaukseksi” (engl. mapping). Mikä tahansa tällainen kuvaus ei kuitenkaan kelpaa todennäköisyydeksi, vaan sen on täytettävä seuraavat aksiomaattiset ehdot [HUOM: aksiomaattisesti määritellyn objektin kaikki ominaisuudet ovat aksioomista johdettavissa].
Määritelmä (aksiomaattinen). Kuvaus \(P:\mathcal{F} \mapsto \mathbb{R}\) tapahtuma-avaruudelta reaaliluvuille on todennäköisyys, jos
\[ \begin{aligned} (1) & \hspace{3 cm} P(A) \ge 0 \text{ kaikilla } A \in \mathcal{F}, \\ (2) & \hspace{3 cm} P(\Omega) = 1, \\ (3) & \hspace{3 cm} \text{Jos } A_i \in \mathcal{F} \ (i = 1, 2, \ldots ) \text{ ja} \\ & \hspace{3 cm} A_i \cap A_j = \emptyset \text{, kun } i \ne j \text{, niin} \\ & \hspace{3 cm} P(\bigcup_{i=1}^{\infty} A_i) = \sum_{i=1}^{\infty} P(A_i). \end{aligned} \tag{2.1}\]
Jälkimmäistä ehtoa kutsutaan täysadditiivisuudeksi. Yhdessä tapahtuma-avaruuden määritelmän kanssa, yllä olevista ehdoista seuraa, että todennäköisyys järkevällä tavalla “mittaa” tapahtumia. Mm., että tapahtuman todennäköisyys on aina nollan ja yhden välissä, ja kahden erillisen tapahtuman yhdistelmä (tapahtuu jotain niiden piirissä olevaa) on aina todennäköisempi (suurempi luku) kuin osatapahtumansa. Meillä on viimein Kolmogorovin todennäköisyysmääritelmän edellyttämät työkalut käytössämme.
Määritelmä. Kolmikko \((\Omega, \mathcal{F}, P)\) on todennäköisyysavaruus, jos \(\Omega\) on ei-tyhjä joukko, \(\mathcal{F}\) on \(\sigma\)-algebra, eli ylläkuvattu tapahtuma-avaruus, ja \(P:\mathcal{F} \mapsto \mathbb{R}\) on todennäköisyys.
Mikä tahansa arkikielen tai kirjallisuuden viittaus “todennäköiseen” tai “mahdolliseen” ei automaattisesti kuvaudu Kolmogorivin matemaattiseksi todennäköisyysavaruudeksi. Käsitteen käyttö satunnaisilmiön kuvailussa edellyttää, että se kytketään teoreettiseen (ajatus)kokeeseen, johon liittyvät käsitteet voidaan kääntää joukko-opin kielelle. Alla oleva listaus havainnollistaa joitain näistä vastaavuuksista, seuraillen Tuomisen (2004) kirjaa.
2.2 Satunnaismuuttuja
Perusjoukon ja erityisesti alkeistapahtuman käsitteet ovat usein todennäköisyysavaruuden soveltajan kannalta hankalia. Persoonallisuuspiirteiden jaukaumia tutkivilla psykologeilla ei ole konsensusta siitä, mikä on persoonallisuuden alkeistapahtuma. Todennäköisyysavaruuden teoreettinen koneisto voi kuitenkin tuntua riittämättömältä jo huomattavasti yksinkertaisemmissakin tapauksissa. Nopanheiton ohella, harhattoman kolikon heitto on klassinen esimerkki todennäköisyysavaruuteen helposti kytkettävästä satunnaisilmiöstä. Tällöin \[ (\Omega, \mathcal{F}, P) = \Big(\big\{kruuna, klaava \big\}, \big\{\emptyset, kruuna, klaava, \{kruuna, klaava\} \big\}, \frac{ \#(A)}{\#(\Omega)} \Big). \] Suurin piirtein tällaista mallia noudattava ihmiselämään liittyvä satunnaisilmiö voisi olla esimerkiksi sukupuoli syntymässä, kun korvataan kruuna naisella ja klaava miehellä. Tässäkin tapauksessa epidemiologit jo tietävät, etteivät tapahtumien “syntyi poika” ja “syntyi tyttö” todennäköisyydet oikeasti ole symmetrisiä, vaan poikien suhteellinen frekvenssi on noin 0,512, ei siis symmetrisyyden edellyttämä 0,5. Vasta satunnaismuuttujan käsite tekee todennäköisyysavaruuden matemaattisesta mallista todella hyödyllisen myös ihmistieteille.
Seuraavassa luvussa käsittelemme satunnaiasmuuttujia ihmistieteissä, mutta tässä luvussa jatkamme vielä määrittelyä havainnollisen ja hyväksitodetun nopanheittoesimerkin avulla. Samalla paitsi esittelemme satunnaismuuttujan myös laajennamme juuri esiteltyä todennäköisyyden käsitettämme. Tätä varten teemme minimaalisen laajennuksen myös noppaesimerkkiin. Rakennamme tällä kertaa mallin kahden nopan heitolle.
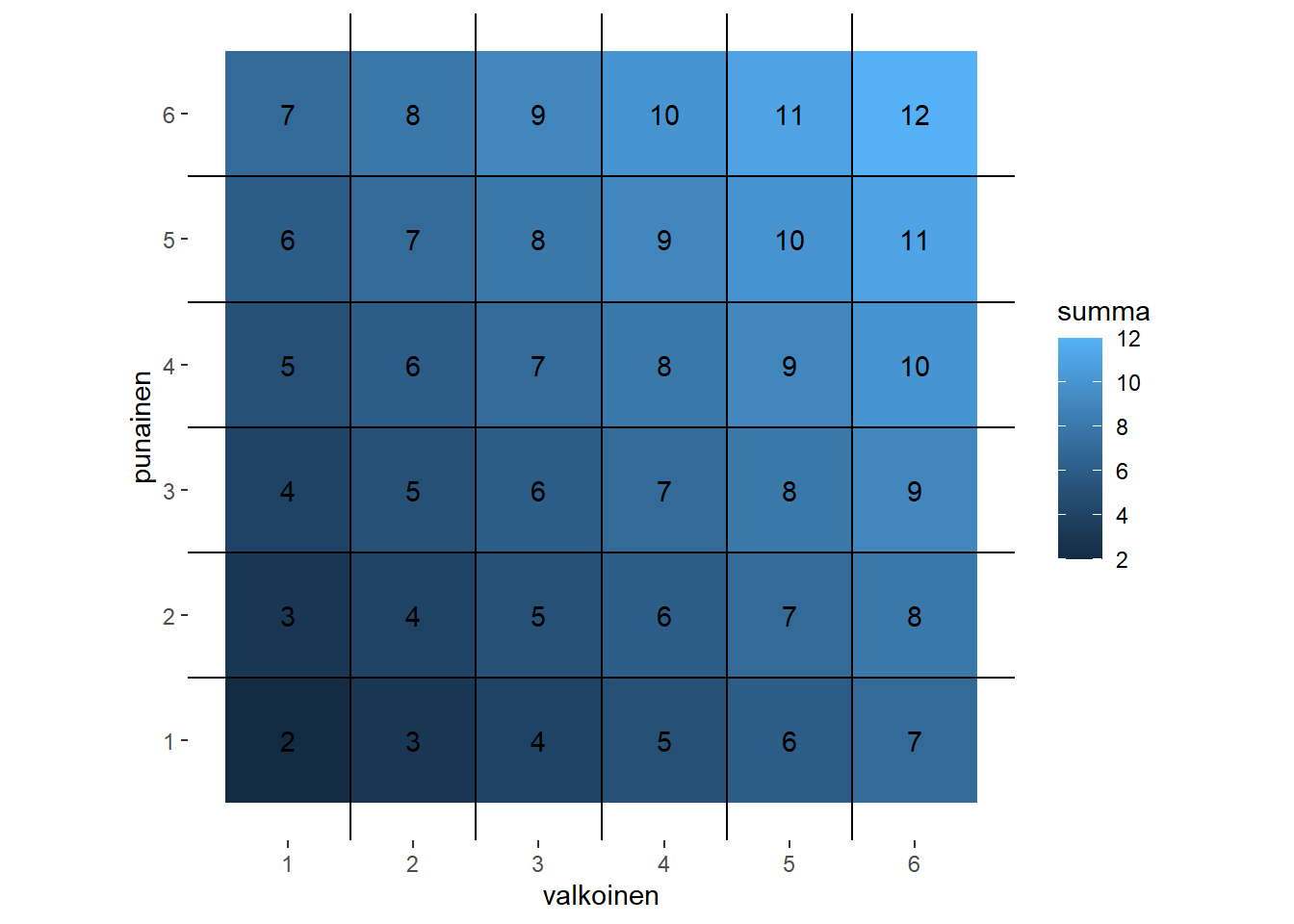
Olkoon ensimmäinen kahdesta nopastamme valkoinen ja toinen on punainen. Tällöin perusjoukon muodostavat alkeistapahtumat ovat järjestettyjä pareja noppien silmäluvuista, esimerkiksi \(\{valkoinen = 1, punainen = 3\}\), lyhyemmin merkittynä \((1, 3)\). Tällaisia järjestetty pareja on yhteensä 36 kappaletta (\(6 \times 6\)). Satunnaisilmiö on helppo mieltää symmetriseksi – jokainen pari (alkeistapahtuma) on yhtä todennäköinen kahden nopan heiton lopputulema. Jokaisen alkeistapahtuman todennäköisyys on \(\frac{1}{36}\). Noppaa pelatessa kuitenkin ollaan usein kiinnostuneita silmälukujen summasta, tarkan järjestyksen sijaan. Tuo summa on epätriviaali esimerkki satunnaismuuttujasta.
Määritelmä. Satunnaismuuttuja \(X\) on (mitallinen) kuvaus (funktio) alkeistapahtumien perusjoukolta \(\Omega\) johonkin toiseen (mitalliseen) avaruuteen (joukolle) \(E\), eli \(X : \Omega \mapsto E\).
“Mitallisuus” on tekninen ehto, jonka ohitamme tässä kohdin. Esimerkiksi, noppasatunnaisilmiössämme \(X(valkoinen, punainen) = valkoinen + punainen\) määrittelee satunnaismuuttujan, joka kuvaa yllämainitun esimerkkialkion \((1, 3)\) kokonaisluvuille kahdesta 12:sta, tarkemmin luvuksi \(X(1, 3) = 1 + 3 = 4\). Satunnaismuuttuja “indusoi” todennäköisyyden maalijoukkoonsa, tässä tapauksessa luvuille \(E = \{2, 3, \ldots, 12\}\). Todennäköisyys kuitenkaan harvoin on symmetrinen maaliavaruuden alkioiden suhteen, vaikka se olisikin sitä satunnaismuuttujan lähtöavaruudessa. Vain yksi noppapari tuottaa alkion \(2 = X(1, 1)\), mutta kaksi paria tuottaa alkion \(3 = X(2, 1) = X(1, 2)\), jne. Alla oleva kuvio tyhjentävästi määrittelee kaikki kahden nopan heiton tapahtuma-avaruuden alkeistapahtumien kuvautumat (summa)satunnaismuuttujan arvoille.

Todennäköisyys ylläkuvatulle maaliavaruudelle saadaan määriteltyä seuraavasti. Kun todennäköisyys tapahtuma-avaruudessamme oli \(P:\mathcal{F}(\{(1,1),(1,2),\ldots,(6,6)\}) \mapsto [0, 1]\), eli kuvaus alkeistapahtumien joukoilta nollan ja ykkösen välille, niin käänteiskuvausjoukot \(\{X \in A\}\) ovat joukon \(\mathcal{F}(\{(1,1),(1,2),\ldots,(6,6)\})\) alkioita, eli “Xn arvo kuuluu joukkoon \(A \in E\)” (merkitään myös \(X^{-1}(A)\)). Todennäköisyys \(P(\{X \in A\})\), tai tavanomaisella lyhennemerkinnällä \(P(X \in A)\), on siis kaikkien \(X\)n joukon \(A\) alkioksi kuvaamien alkeistapahtumien joukon koko suhteessa kaikkiin alkeistapahtumiin. Usein tätä merkitään
\[ P(\{\omega \in \Omega:X(\omega) \in A \}), \]
missä tapahtuma-avaruuden joukko luetaan “jokainen perusjoukkoon kuuluva alkeistapahtuma siten, että satunnaismuuttuja \(X\) kuvaa sen joukkoon \(A\)”.
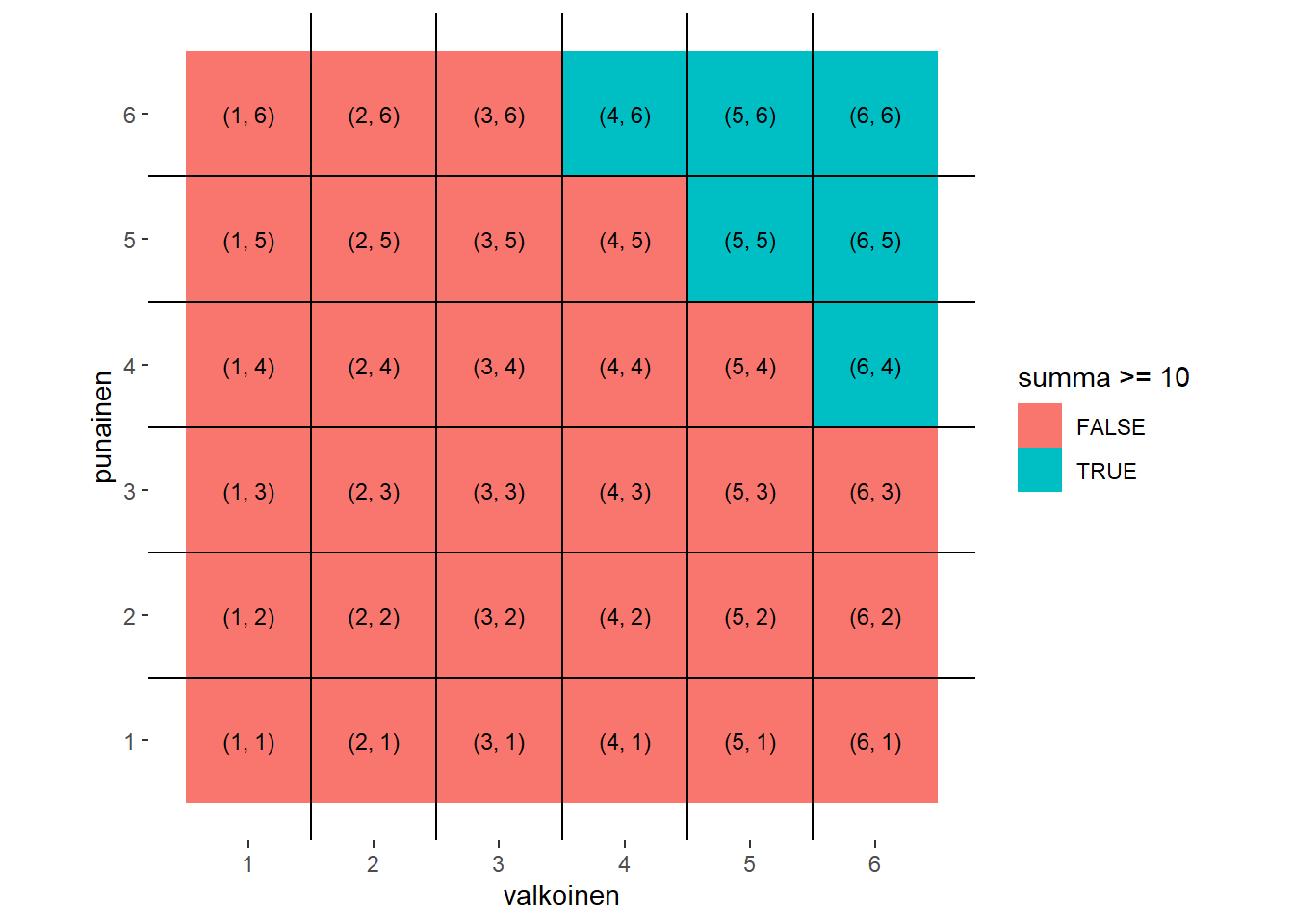
Ajatellaan esimerkiksi tapahtumaa “kahden nopan silmälukujen summa on 10 tai enemmän”, eli \(\{X \ge 10\}\), mitä voidaan tarkemmin merkitä myös \(\{\omega : X(\omega) \in \{10, 11, 12\}\}\), tässä tapauksessa tarkoittaen \(\{(valkoinen, punainen) : valkoinen + punainen \ge 10\}\). Alkuperäisen symmetrisen todennäköisyysmallin indusoima tapahtuman todennäköisyys on \(P(\{X \ge 10\}) = \frac{\#(\{\omega : X(\omega) \in \{10, 11, 12\}\})}{\#(\Omega)}\), eli satunnaismuuttujan tapahtuman toteuttavien alkeistapahtumien lukumäärän suhde kaikkiin alkeistapahtumiin. Alla oleva kuva havainnallistaa tätä suhdetta. Nähdään, ettei se vastaa symmetristä kolmen alkion suhdetta 11:sta \(X\):n maaliavaruuden mahdolliseen alkioon (arvoa \(\frac{3}{11} \approx 0.27\)), vaan tapahtuman todennäköisyys on \(\frac{6}{36} = \frac{1}{6} \approx 0.17\).
Nyt satunnaisilmiön mallimme teoreettisesti ja tarkasti ennustaa koko satunnaismuuttujan \(X\) ns. diskreetin todennäköisyysjakauman. R-kielessä voimme piirtää sen kuvaajan (ks. alla) alla olevalla koodilla. Kuvaajasta nähdään, että \(X\):n arvot ovat kaukana symmetrisestä ja, että todennäköisin kahden nopan summapiste on 7. Jo noppaesimerkki osoittaa, että satunnaismuuttujien avulla teoreettisesti mallista voidaan johtaa epätriviaaleja ja kiinnostavia ennusteita. Empiirisesti orientoituneelle lukijalle tälläinen deduktiivinen päättely premisseistä voi kuitenkin tuntua vieraammalta kuin induktiivinen päättely aineistosta. Satunnaismuuttuja näyttelee avainroolia näiden traditioiden yhdistämisessä!
d <- expand.grid(valkoinen=1:6, punainen=1:6) # perusjoukko
X <- function(valkoinen, punainen) valkoinen + punainen # satunnaismuuttuja
lkm <- table(X(d$valkoinen, d$punainen)) # alkeistapahtumien lkm
tiheys <- lkm/sum(lkm) # lopputulema-tiheys
barplot(tiheys, names.arg = names(tiheys), # tn-jakauman kuva
xlab = "valkoinen + punainen", ylab = "Suhteellinen frekvenssi")
# Lasketaan P(X>=10) tn-ominaisuuden (3) avulla
as.numeric(tiheys["10"] + tiheys["11"] + tiheys["12"])[1] 0.1666667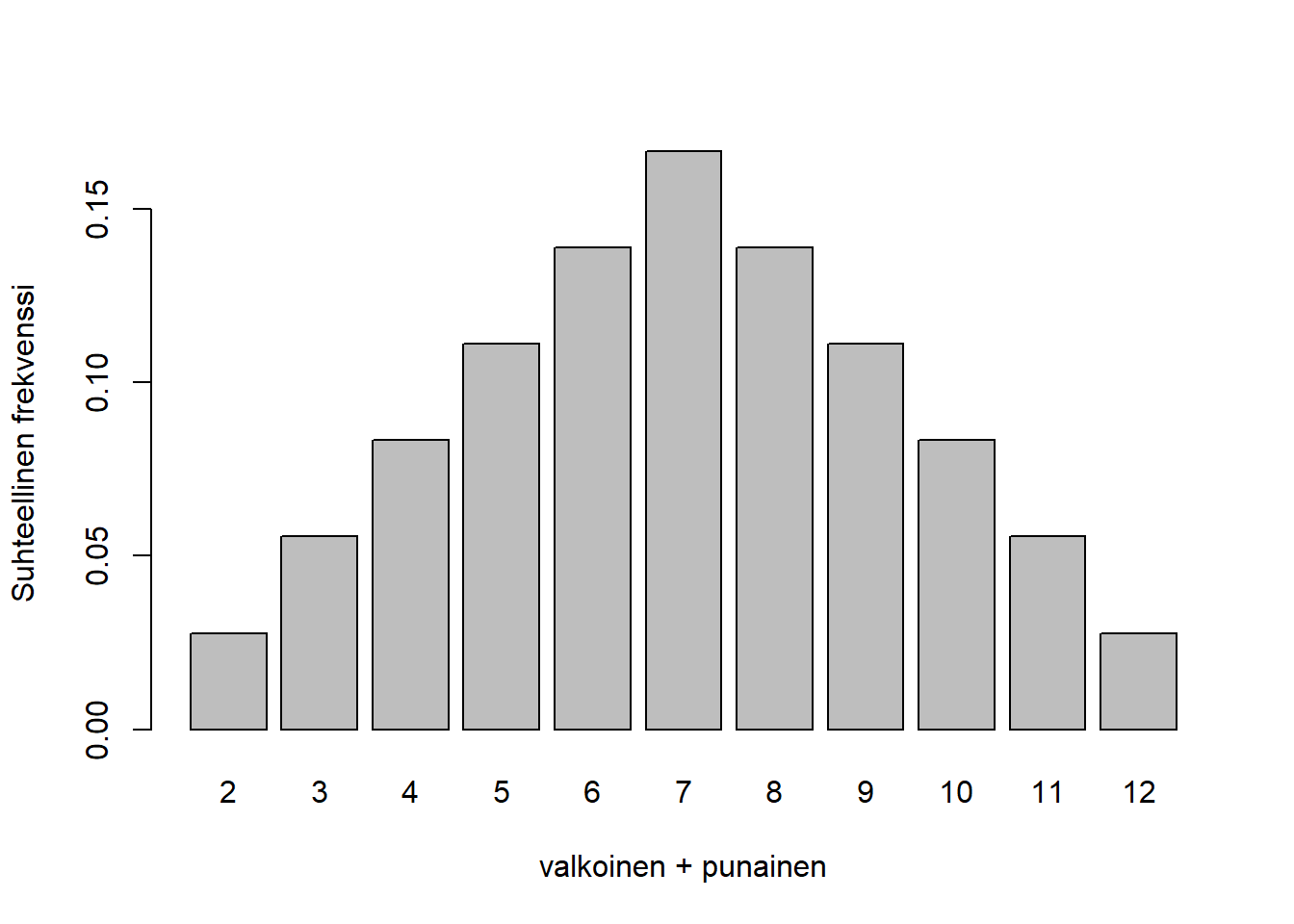
Empiiriselle terveyden alan tutkijalle tavanomaisessa määrällisessä analyysissa jokin tosimaailman koe tai aineisto on tuottanut jakauman jonkin “satunnaismuuttujan” \(X\) arvoja. Lainausmerkit tässä tarkoittavat, että tutkija haluaa tulkita havaintonsa heijastelevan jotain satunnaisilmiötä tai koetta. Tällöin myös tuntematta tarkkaa todennäköisyysavaruutta, voidaan luottaa taustalla olevan jonkin satunnaismekanismin joku tuon empiirisen jakauman indusoi – tutkija siis tutkii jotain todellista mekanismia satunnaismuuttujan kautta, tietäen sille pätevän alla kuvatun lainalaisuuden (todennäköisyys on yhdistetty funktio!).
Kuva 2 nostaa esiin muutamia olennaisia huomioita. Ensinnäkin, satunnaismuuttuja kuvaa perusjoukon alkioita maaliavaruuteensa siten, eikä sen tarvitse olla “kääntyvä” funktio – tässä \(X\) kuvaa kokonaisen joukon alkioita \(A \subset \Omega\) yhdeksi pisteeksi \(e \in E\) (Huom! \(A \in \mathcal{F}\)). Funktio toimii toki alkio (\(a \in \Omega\)) kerrallaan, mutta esimerkissä kuvaa siis kaikki \(A\):n alkiot samaksi arvoksi \(e\). Se voi kuvata myös kaikki joukon \(B\) alkiot samaksi arvoksi \(e\), jolloin \(e\):n käänteiskuva on kaikki molempien joukkojen alkiot, jotka voivat olla osin päällekkäisiäkin, eli \(X^{-1}(e) = A \cup B\). Näin alkuperäinen todennäköisyys \(P\) voi olla hienojakoisempi ja sillä voidaan eritellä tapahtumat \(A\) ja \(B\), kun taas \(X\):n siitä indusoima todennäköisyys “näkee” vain yhdistetapahtuman \(A \cup B\). Kuva näyttää useita merkintätapoja tapahtuman \(\{X = e\}\) todennäköisyydelle. Voidaankin (ja myös täytyy) ajatella, että maaliavaruudessa on jokin tapahtuma-avaruus, \(\sigma\)-algebra \(\sigma(E)\), ja indusoitu todennäköisyys on funktio \(P_X : \sigma(E) \mapsto [0, 1]\).
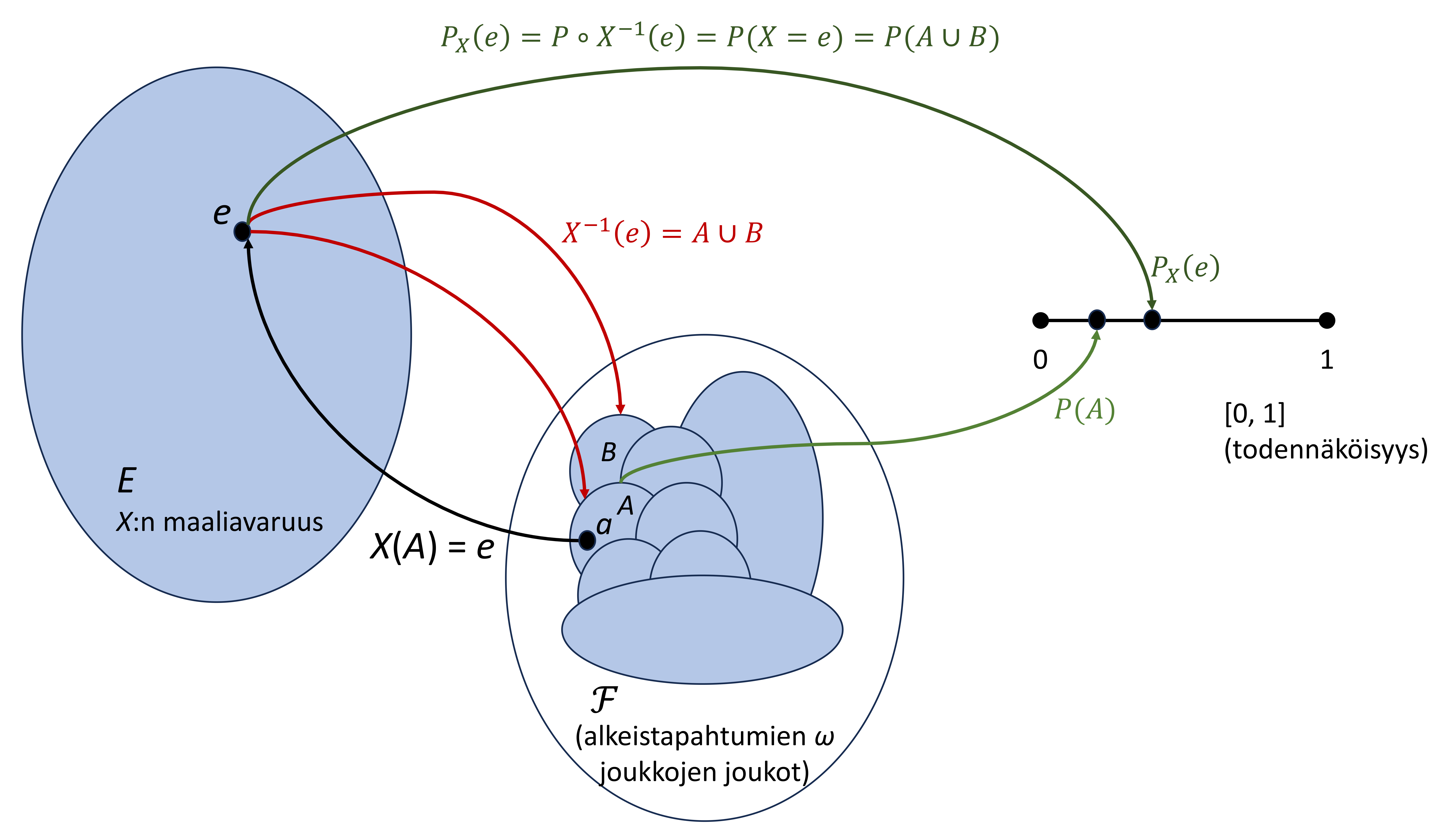
Terveystieteiden empiirisissä tarkasteluissa käsittelemmekin siis lähes yksinomaan indusoituja todennäköisyyksiä. On silti hyödyllistä tuntea taustalla vaikuttava matemaattinen malli. Siitä voi toisinaan saada alakohtaistakin sisällöllistä näkemystä. Ennen muuta se tietysti on tärkeää sovelletun tilastoteorian ymmärtämiseksi. Seuraavassa osiossa tarkastelemme joitain sovelluksista nousevia indusoituja todennäköisyyksiä, eli jakaumia, ja esittelemme samalla satunnaismuuttujan jakauman ja odotusarvon käsitteitä. Sitä seuraavassa osiossa taas käsittelemme joitain tilastotieteen keskeisimpiä näitä koskevia tuloksia, kuten keskeistä raja-arvolausetta. Lopulta nämä kytketään esimerkinomaisesti tilastolliseen mallintamiseen ja testaamiseen. Tässä osiossa tarkastelemme vielä riippumattomuuden käsitettä.
2.3 Riippumattomuus
Tapahtumat voivat olla toisistaan riippumattomia. Esimerkiksi yllä, valkoisen nopan silmaluku ei riipu siitä mitä punaisesta nopasta sattui tulemaan.
Määritelmä (riippumattomuus). Todennäköisyysavaruuden \((\Omega, \mathcal{F}, P)\) kaksi tapahtumaa \(A\) ja \(B\) ovat riippumattomia, kun pätee \(P(A \cap B) = P(A)P(B)\). [tapahtumaa \(P(A \cap B)\), eli “tapahtuu sekä A että B”, merkitään usein myös \(P(A, B)\)].
Kääntäen, jos tapahtumat eivät ole riippumattomia, ne ovat riippuvia. Esimerkiksi, jos ajatellaan satunnaismuuttajaa \(Y = \max(X_{\text{valkoinen}}, X_{\text{punainen}})\), tapahtuma “\(Y\) on enintään \(y\)” on sama kuin tapahtuma “\(X_{\text{valkoinen}}\) ja \(X_{\text{punainen}}\) on enintään \(y\)”. Symbolein, \(P(Y \le y) = P(\{X_{\text{valkoinen}} \le y \} \cap \{X_{\text{punainen}} \le y \}) = P(X_{\text{valkoinen}} \le y)P(X_{\text{punainen}} \le y)\). Tällöin ei voi päteä, että esimerkiksi tapahtumat \(\{Y \le 2\}\) ja \(\{X_{\text{valkoinen}} \le 2\}\) olisivat riippumattomia. Jos esim. valkoisesta nopasta tulee silmäluku kolme (\(\{X_{\text{valkoinen}} \le 2\}\) ei päde), tulee myös tapahtumasta \(\{Y \le 2\}\) mahdoton. Valkoisen ja punaisen nopan maksimi ei voi olla alle kolme, jos valkoisen silmäluku oli kolme. Riippumattomaatta voidaankin lähestyä myös ehdollisen todennäköisyyden näkökulmasta. Jos tapahtuman \(A\) todennäköisyys ehdolla, että \(B\) tapahtuu, eli \(P(A|B)\), on yhtä kuin \(P(A)\), on tapahtuma \(A\) riippumaton tapahtumasta \(B\).
Määritelmä (ehdollinen todennäköisyys). Tapahtuman \(A\) todennäköisyys ehdolla, että tapahtuma \(B\) sattuu, on \[ P(A|B) = \frac{P(A \cap B)}{P(B)}. \]
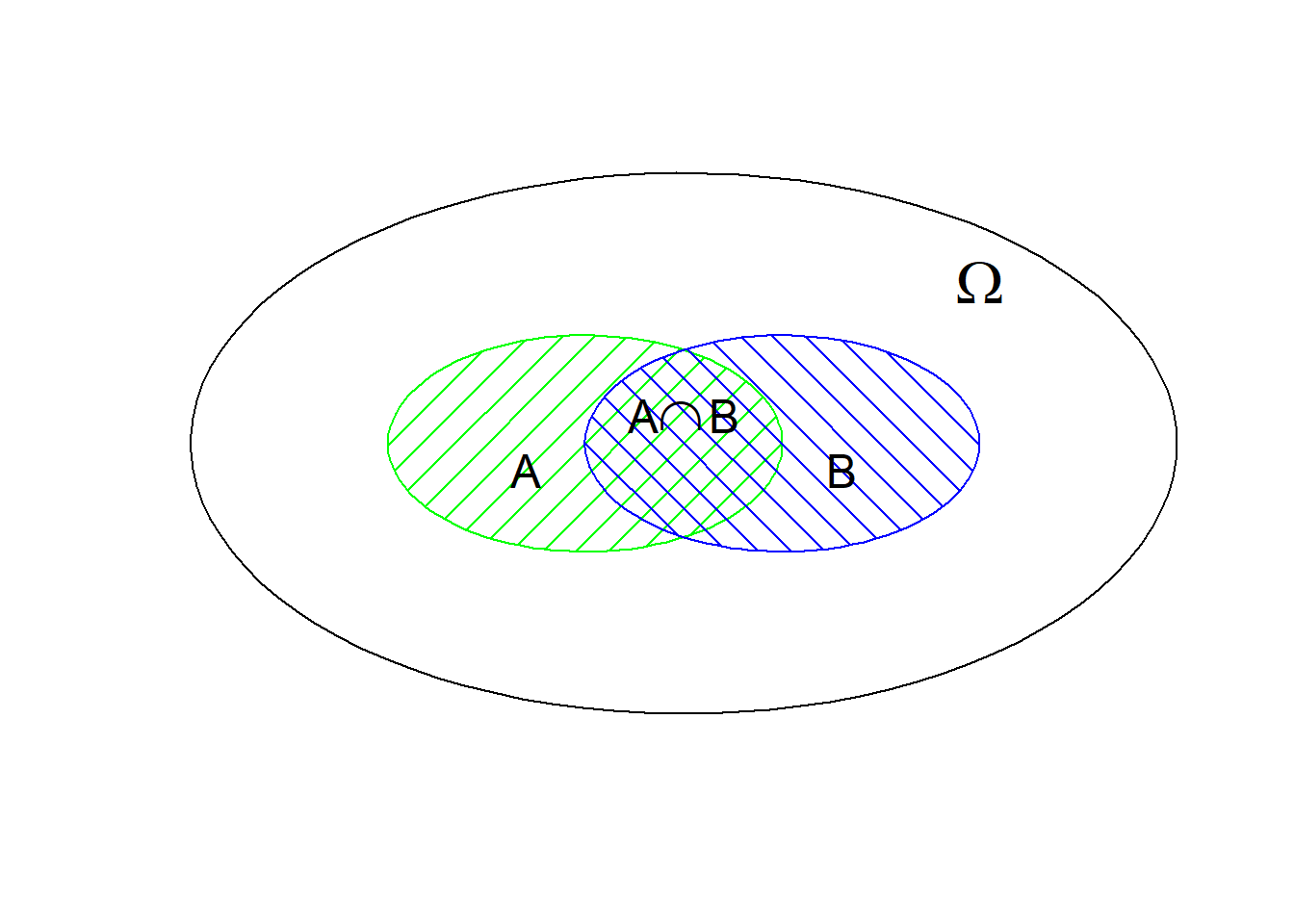
Määritelmän logiikka on nähtävissä, kun huomataan, että \(P(A) = P(A|\Omega) = \frac{P(A \cap \Omega)}{P(\Omega)} = \frac{P(A)}{1}\), koska aina pätee \(A \subset \Omega\) ja \(P(\Omega)=1\). Eli siinä missä tavallinen todennäköisyys vertaa tapahtuman sisältämiä alkeistapahtumia perusjoukon alkeistapahtumiin, ehdollinen todennäköisyys \(P(A|B)\) vertaa tapahtuman “sattuu \(A\) ja \(B\)” alkeistapahtumia tapahtuman “sattuu \(B\)” alkeistapahtumiin. Toisin sanoen, perusjoukko rajataan tapahtuman \(B\) toteuttaviin alkeistapahtumiin. Alla oleva Venn-diagrammi havainnollistaa asiaa. Todennäköisyys \(P(A \cap B)\) vertaa tapahtuman \(\{A \cap B\}\) “kokoa” perusjoukon \(\Omega\) kokoon, mutta ehdollinen todennäköisyys \(P(A|B)\) vertaa tapahtuman \(\{A \cap B\}\) “kokoa” joukon \(B\) kokoon. Jälkimmäisessä tapauksessa ajatellaan, että \(B\):n tiedetään tapahtuvan, eli joku sen alkeistapahtumista toteutuu ja kysymys on enää siitä kuuluuko toteutuva tapahtuma myös leikkausjoukkoon \(\{A \cap B\}\).
Kertomalla yllä oleva ehdollisen todennäköisyyden määritelmän yhtälö arvolla \(P(B)\) molemmin puolin yhtäsuuruusmerkkiä ja vertaamalla riippumattomuuden määritelmään, nähdään, että riippumattomuuden määritelmäksi voidaan yhtä hyvin ottaa myös yllä sivuttu yhtälö \(P(A|B) = P(A)\). Esimerkiksi, koska \(\{ X_{\text{valkoinen}} \le 3\} \cap \{ X_{\text{punainen}} \le 3\} \subset \{ X_{\text{valkoinen}} \le 3\}\) yllä määritellylle maksimille pätee \[ \begin{aligned} P(Y \le 3, X_{\text{valkoinen}} \le 3) &= P(Y \le 3) \\ &= P(X_{\text{punainen}} \le 3)P(X_{\text{valkoinen}} \le 3) \\ &= \frac{3}{6} \times \frac{3}{6} \\ &= \frac{1}{4}. \end{aligned} \] Arvo on eri suuri kuin \(\frac{1}{4} \times \frac{3}{6} = P(Y \le 3)P(X_{\text{valkoinen}} \le 3)\). Tapahtumat \(\{Y \le 3 \}\) ja \(\{ X_{\text{valkoinen}} \le 3 \}\) voidaan siis todeta riippuviksi alkuperäisen määritelmän nojalla. Riippuvuuden määrää voidaan arvioida ehdollisen todennäköisyyden avulla. Määritelmään sijoittamalla nähdään, että \(P(Y \le 3 | X_{\text{valkoinen}} \le 3) = \frac{\frac{3}{6} \times \frac{3}{6}}{\frac{3}{6}} = \frac{1}{2}\), kun taas riippumattomuus tuottaisi yo. arvon \(\frac{1}{4}\).
2.3.1 Kokonaistodennäköisyyden laki ja Bayesin kaava
Ehdollisen todennäköisyyden määritelmästä seuraa suoraan myös ns. kokonaistodennäköisyyden laki. Yllä olevasta Venn-diagrammista on helppo todetä, että \(A\) koostuu aina osasta, jonka se jakaa jonkin joukon \(B\) kanssa ja osasta, jota se ei jaa (eli jakaa \(B\):n komplementin kanssa; huom., leikkaukset saavat olla tyhjiäkin joukkoja). Joukko voidaan siis osittaa kahteen leikkausjoukkoon: \(A = \{A \cap B\} \cup \{A \cap B^c \}\). Nämä osat ovat erillisiä. Siten todennäköisyyden aksioomista seuraa, että \(P(A) = P(A \cap B) + P(A \cap B^c)\). Näin ollen ehdollisen todennäköisyyden määritelmästä seuraa, että \[ P(A) = P(A|B)P(B) + P(A|B^c)P(B^c). \tag{2.2}\] Havainto yleistyy siten, että jos joukot \(\{B_1,B_2, \ldots, B_K\}\) ovat perusjoukon \(\Omega\) ositus erillisiin osajoukkoihin, niin \(P(A) = \sum_{i=1}^K P(A|B_i)P(B_i)\). Tämä on hyödyllistä silloin, kun emme pysty laskemaan tapahtuman \(A\) todennäköisyyttä, mutta pystymme laskemaan muotoa \(P(A|B_i)P(B_i)\) olevia lukuja. Esimerkiksi ehdollisen todennäköisyyden symmetriasta \(P(A|B)P(B) = P(A \cap B) = P(B|A)P(A)\) seuraa ns. Bayesin kaava käänteistodennäköisyyden laskemiseen: \[ P(B|A) = \frac{P(A|B)P(B)}{P(A)}. \] Jos \(A\) on esimerkiksi tietty havaintoaineisto, joka meillä on, on usein mahdotonta tietää sen todennäköisyys. Havaitsemiseen saattaa liittyä ainutlaatuisia tilanteita. Jos kuitenkin tapahtumien \(\{B_1,B_2, \ldots, B_K\}\) ajatellaan edustavan todennäköisyyksiä, että aineiston on synnyttänyt malli 1, 2, …, tai K, ja aineiston saamisen todennäköisyys \(P(A|B_i)\) voidaan laskea kullekin mallille, luku \(P(A) = \sum_{i=1}^K P(A|B_i)P(B_i)\) on laskettavissa. Tässä toki tehdään oletus, että aineiston synnyttänyt malli on joku malleista 1, 2, …, tai K. Tällöin ovat myös laskettavissa mallien a posteriori todennäköisyydet \(P(B_i|A)\). Tässä kontekstissa lukua \(P(A|B_i)\) kutsutaan aineiston tarjoamaksi evidenssiksi mallille \(i\) ja lukua \(P(B_i)\) mallin (subjektiiviseksi) a priori todennäköisyydeksi. Koska termi \(P(A)\) pysyy vakiona mallien keskinäisessä vertailussa, Baeysin kaavasta seuraa kuuluisa verrannollisuussuhde \[ P(\text{ malli }|\text{ aineisto }) \propto \text{ aineistoevidenssi } \times \text{ edeltävä uskomus .} \] Bayes-laskenta siis antaa todennäköisyyksiä malleille ja uskomuksille, eroten ns. frekventistisestä tilastotieteestä, joka vain olettaa mallin ja laskee sen mukaisen aineistoevidenssin ja evidenssiä koskevien hypoteesien todennäköisyyksiä. Kumpikin tilastoparadigma on tällä kurssilla käsitellyn (todennäköisyys)teorian sovellutus.
JATKA SATUNNAISMUUTTUJAN ABSTRAKTEIHIN ESIMERKKEIHIN ERI LUVUSSA. SITTEN MUUT SISÄLLÖT.
INTROA KESKEINEN RAJA-ARVOLAUSE KOLMELLA NOPALLA, YLTÄ JATKAEN.