Research papers | Supplementary videos | Slides of talks |
We are studying mathematical inverse problems for non-linear wave equations and the Einstein equations coupled with scalar field equations. Roughly speaking, the problem we have considered is the following: Can an observer do local measurements to determine the structure of the space-time in the maximal region where the waves can propagate from its world line and return back? On this topic are writing a series of papers. The first paper in this series is
A supplementary video is below.
The paper 1 concers scalar non-linear wave equations and it combines the results of our earlier Arxiv-preprints
In these papers we show that the inverse problem for active measurements for non-linear wave equation or for the Einsten system can be reduced to the inverse problem for passive measurements. This passive measurement problem is solved using techniques of global Lorentzian geometry. In addition to relativity, the techniques have applications in medical imaging methods based on non-linear hyperbolic equations, in particular in quantitative elastography. In astronomy, the passive measurements are related to long-observation time observations of variable stars and gravitational wave astronomy.
The papers have three supplementary animations:
In the first supplementary video we show the geometric situation when three plane waves propagate in space and collide. In the second and third supplementary videos we show the collision of four plane waves.
The plane waves are singular on hyperplanes of the 4-dimensional space-time (the Minkowski space). When the planes intersect, the non-linearity of the hyperbolic system produces new waves.
Video 1: When three plane waves collide, the intersections of the hyperplanes is a 1-dimensional space-like line in the 4-dimensional space-time. This corresponds to a point moving continuously in time. Roughly speaking, the point seems to move at a higher speed than light and produces a (conic) singularity that is geometrically analogous a shock wave.
Video 2: When four plane waves collide, the intersections of the four hyperplanes is a point in the 4-dimensional space-time. This point becomes a virtual point source that produces a spherical wave. Note that in video 2 only one conic wave of the four conic waves produced by 3-interactions is shown. This is done to make the appearance of the spherical wave, produced by the virtual point source, easier to see. The events in the video are explained in the pictures and the text below.




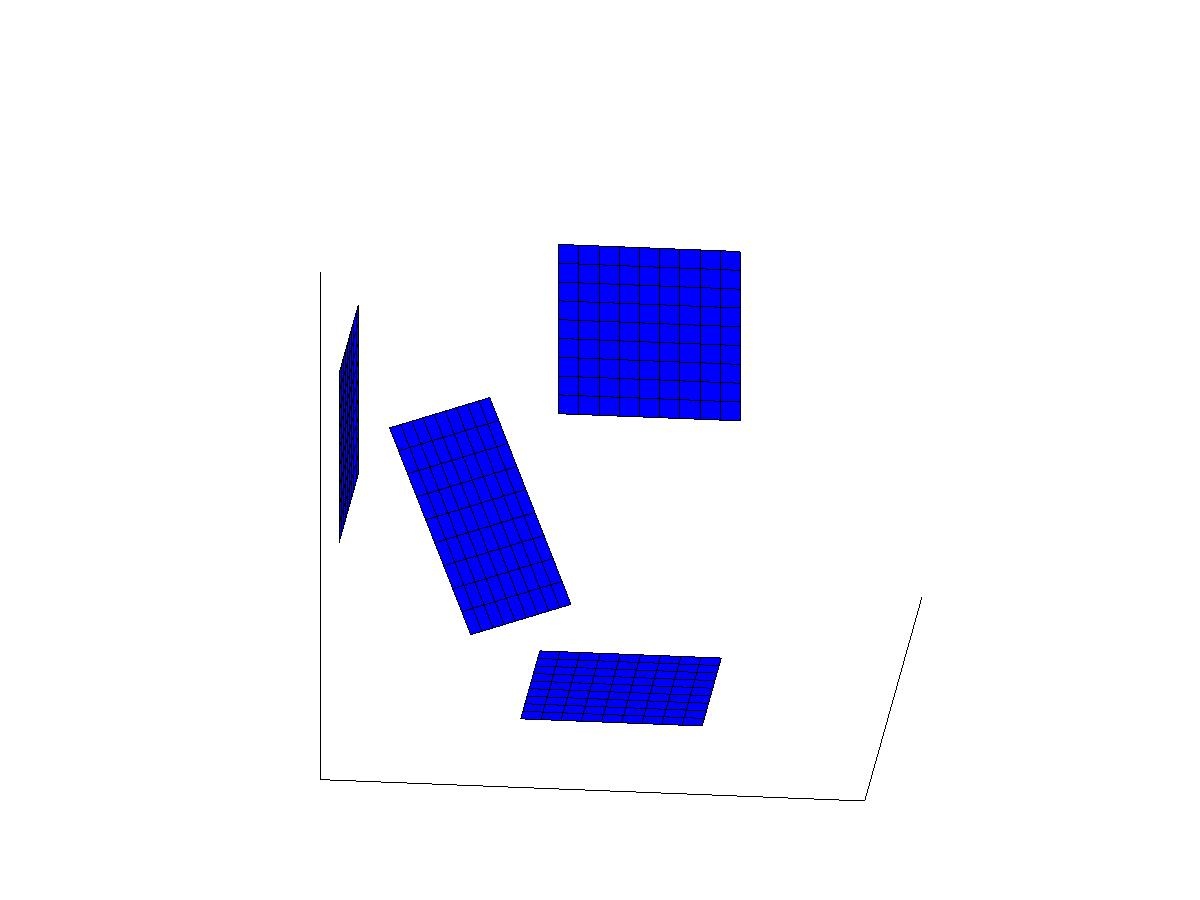
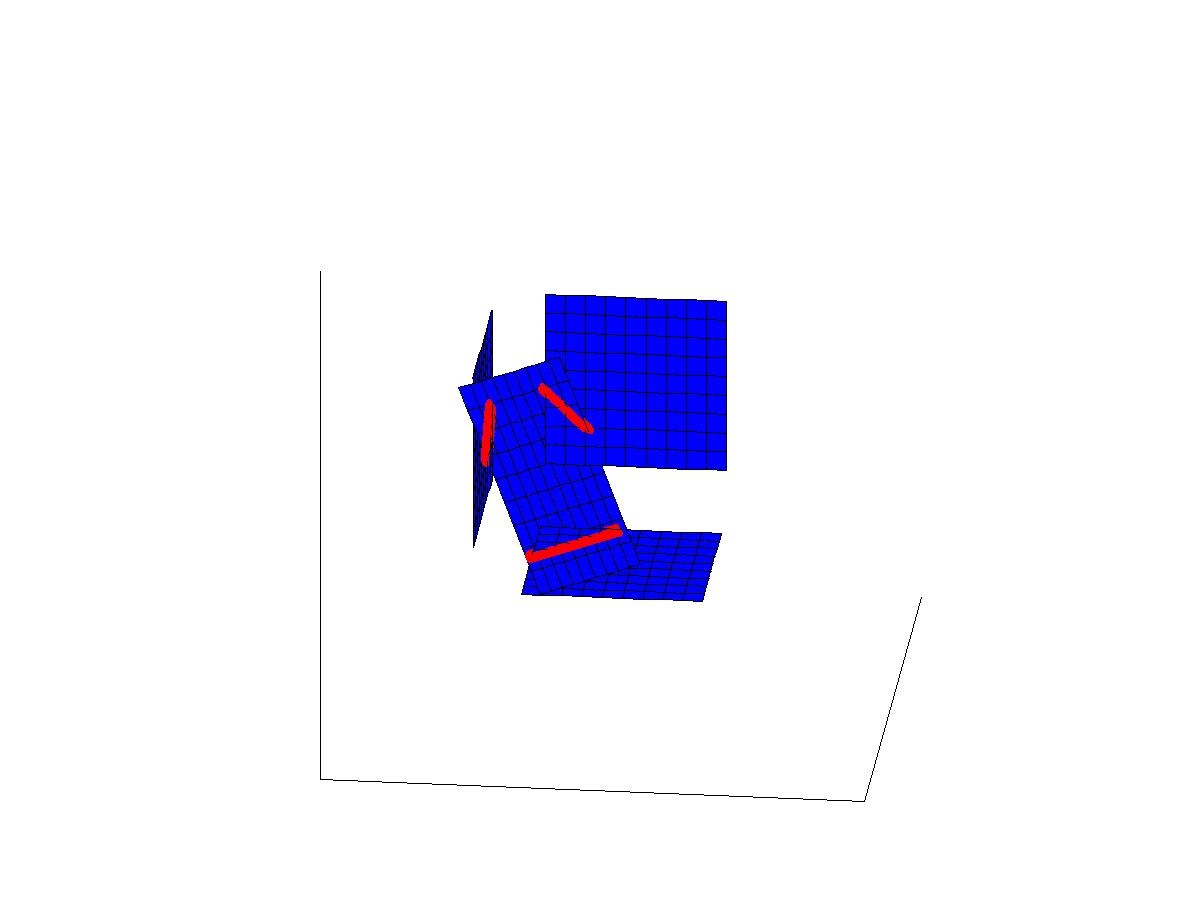
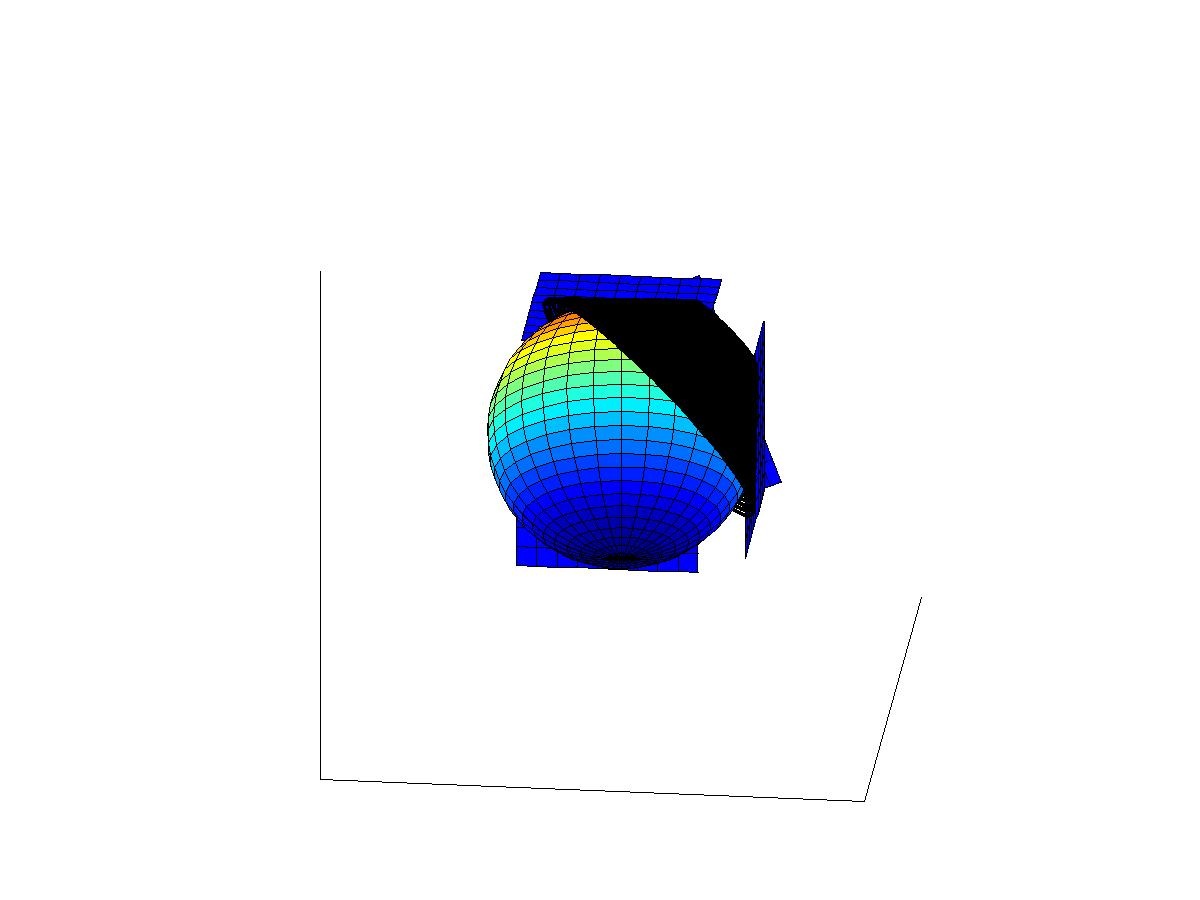
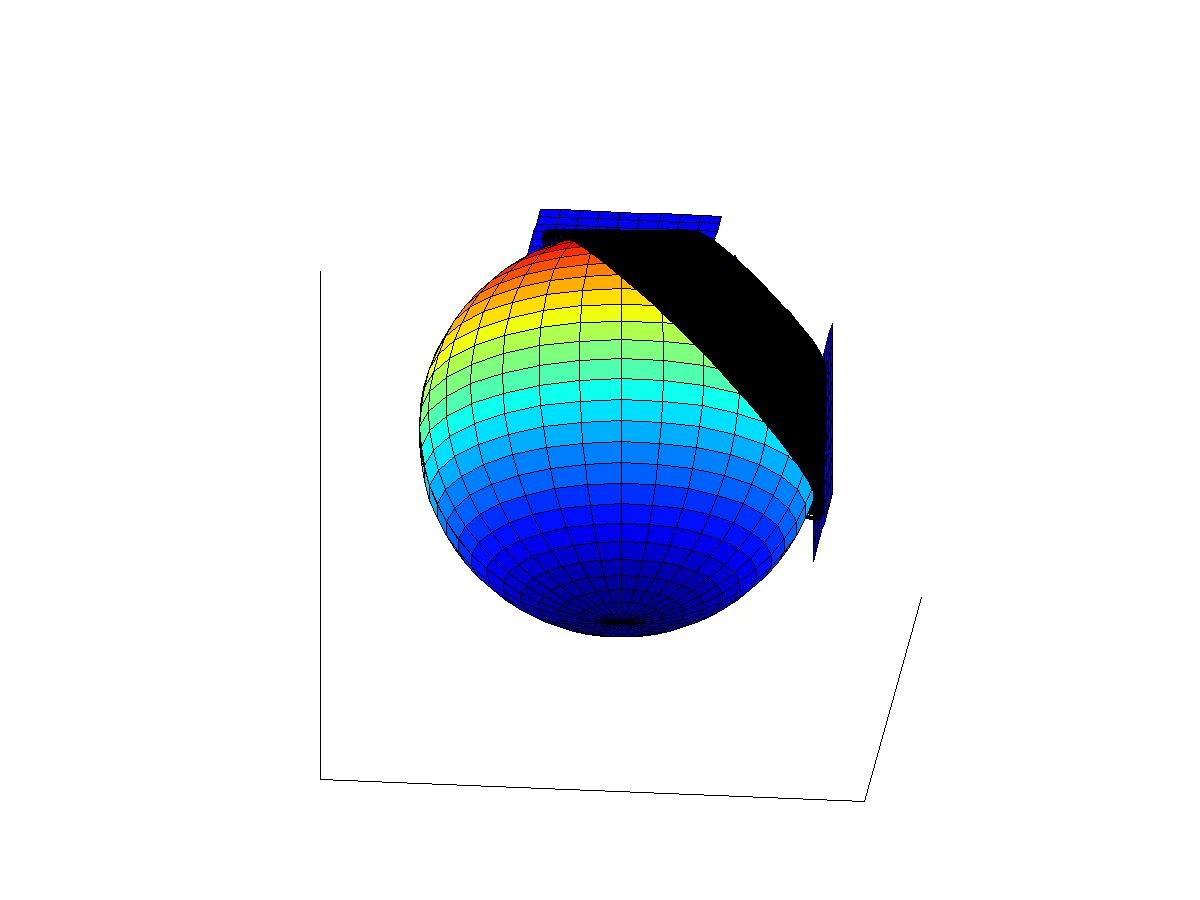
The four above figures show the waves before the interaction of the waves start, when 2-wave interactions have started, when all 4 waves have just interacted, and later after the interaction. More presicely, the figures show the following situations:
1st figure: Plane waves before interacting.
2nd figure: The 2-wave interactions (red line segments) appear but do not cause new propagating singularities.
3rd and 4th figures: All plane waves have intersected and new waves have appeared. The 3-wave interactions cause new conic waves (black surface). Only one such wave is shown in the figure.
The 4-wave interaction causes a point source in space-time that sends a spherical wave in all future light-like directions. The interaction of four waves can be considered as an artifical point source (or an "artificial star") in the space time. Assume now that one can produce the distorted plane waves using sources supported in a domain U of the space-time. Then, the artificial point source corresponding to the interaction of the distorted plane waves can produced at any point of the space time. Thus, the spherical waves caused by artificial point sources are considered as data for the inverse problem for the passive measurements. In the paper 2 we show that this data determines the conformal type of the Lorentzian metric in a diamond type set containing the freely falling observer near which one can both produce the sources and observe the waves.
Video 3: In video 3 four pieces plane waves interact similarly as in video 2, but the width of these pieces of plane waves is smaller. Thus the interaction time of the waves is smaller. In particular, the width of the conic waves produced by the 3-interaction is smaller. We point also out that when the width of the pieces of plane waves goes to zero, the black conic waves approach to circles moving in the time. In video 3, all conic waves produced by 3-interactions (black cones) are visible. Note that there are four conic waves but one of those is not visible as it is behind the sphere.
The slides are the presentation given on the inverse problems for the Einstein equation at conference at CIRM, Luminy, France.
Matti Lassas <Matti.Lassas helsinki.fi>
helsinki.fi>
November 25, 2017