Fysiikan laitos
Opettajien
laboratoriokurssit
kevät 2013
|
|
Fysiikan laitos Opettajien
laboratoriokurssit |
Taulukkolaskenta (spreadsheet) on alun alkaen liike-elämän tarpeisiin kehitetty ohjelmatyyppi. Ohjelma näyttää kuvaruudulla laskenta-arkin, joka on jaettu riveihin ja sarakkeisiin viivoitetun paperin tapaan. Sarakkeet nimetään yleensä kirjaimilla, rivit numeroilla. Yksittäisiä ruutuja kutsutaan soluiksi. Solun sarake ja rivi yksilöivät solulle tunnuksen, esim. A1 tai F13. Solu sisältää yleensä joko luvun, tekstiä, tai laskentakaavan. Jos solu sisältää luvun tai tekstiä, solun arvo on sama kuin solun sisältö. Jos solu sisältää kaavan, solun arvo on kaavaan sijoituksen tulos. Kaavat käyttävät laskennan lähtöarvoina kaavan sisältämiä lukuja sekä toisten solujen arvoja. Rivien tai sarakkeiden sisältämistä lukusarjoista voidaan piirtää graafisia kuvaajia. Taulukkolaskenta soveltuu luonnontieteelliseen laskentaan ja tulosten esittämiseen silloin, kun laskentatyökalulta vaaditaan helppokäyttöisyyttä, ja dataa on suhteellisen vähän. Nykyisin taulukkolaskennan perusteet opitaan koulun ATK-opetuksen yhteydessä.
Lasketaan painopisteen paikka kolmesta kappaleesta koostuvalle yksiulotteiselle systeemille.
Tunnetusti tällaisen systeemin massakeskipisteen paikkavektori saadaan lausekkeesta
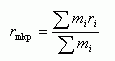
Sijoitetaan kappaleiden paikkavektorit ja massat sekä kaava laskenta-arkkiin:
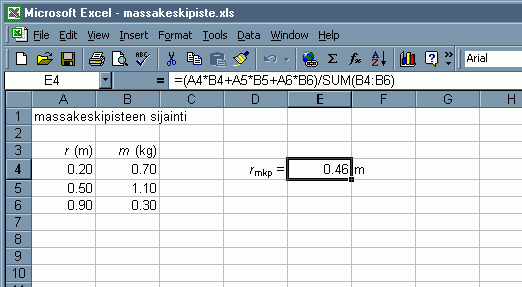
Esimerkkitaulukossa solut A1, A3, B3, D4 ja F4 sisältävät tekstiä, solut A4:B6 sisältävät lukuja, ja solu E4 sisältää laskentakaavan. Solu E4 on valittuna, joten sen sisältämä kaava näkyy syöttörivillä.
Windows- ja Mac-ympäristöissä Microsoft Excel on ylivoimaisesti eniten käytetty taulukkolaskin.
Excelin merkittäväksi haastajaksi on noussut OpenOffice / LibreOffice, joka on saatavissa Windows-, Linux-, Mac- Ja Solaris-ympäristöön. Ohjelmiston taulukkolaskentaosuus on puhtaan laskennan osalta pitkälti Excel-yhteensopiva. Uusimmissa versioissa myös grafiikan ominaisuudet on vihdoin saatu opetuskäyttöön riittävälle tasolle. LibreOffice on ilmainen ja avoin.
Suurin osa alla olevasta on sovellettavissa suoraan sekä Excelissä että LibreOfficessa. Yksityiskohtaisemmissa ohjeissa esimerkkiohjelmana on suomenkielinen OpenOffice 3.0. uudemmat LibreOfficet toimivat pääosin samoin.
Yksinkertaisin tapa tuoda mittaustulokset taulukkolaskimeen on kopioda luvut käsin. Joskus käsin kopiointi on ainoa mahdollisuus mittausohjelman omilla laskentatyökaluilla (esim. suoran sovituksella) saatujen arvojen siirtämisessä. Se on kuitenkin hidasta ja virhealtista, joten menetelmä on järkevä vain silloin kun siirrettäviä lukuja on vähän.
Mittaustietoa voidaan yleensä siirtää mittausohjelman taulukkoesityksestä taulukkolaskimeen kopioi-liitä -menetelmällä leikepöydän kautta. Tiedonsiirto onnistuu tällä tavalla Logger Pro- ja DataStudio -mittausohjelmista. Pieniä ongelmia voi seurata siitä että vanhemmat Logger Pro:n 2.x -versiot (sekä betatestivaiheessa oleva Linux-versio) käyttävät aina desimaalipistettä, kun taas taulukkolaskimet käyttävät koneen maa-asetuksista riippuen joko pistettä tai pilkkua. Tarvittaessa pisteet voi muuttaa pilkuiksi taulukkolaskimen etsi-korvaa -toiminnolla. Windowsissa Logger Pro 3 ja uudemmat käyttävät maa-asetuksissa valittua desimaalierotinta.
Tiedonsiirtoon voidaan käyttää myös välitiedostoja. Siirtoon täytyy käyttää sellaista tiedostomuotoa, jota mittausohjelma osaa kirjoittaa ja taulukkolaskin osaa lukea. Kaikki taulukkolaskimet osaavat lukea tekstimuodossa olevaa dataa. Tekstirivit tulkitaan taulukon riveiksi, tabulaattorimerkit tulkitaan sarakerajoiksi. Toisaalta kaikki mittausohjelmat osaavat tallettaa datan levylle tekstinä, mutta tiedostoa saattaa olla tarpeen editoida käsin, jotta taulukkolaskin tulkitsisi tiedoston oikein.
Mittausdatasarjat esitetään taulukkolaskimessa yleensä sarakkeina. Jos on vaikkapa mitattu suureen arvoa ajan funktiona, yhdessä sarakkeessa ovat ajan hetket ja viereisessä sarakkeessa vastaavat suureen arvot.
Datasarjasta voidaan
laskea yksittäinen tulos (esim. keskiarvo tai integraali),
muutamasta arvosta koostuva tulos (esim. funktion sovitus, tuloksena
termien kertoimet), tai sitten voidaan laskea kokonaan uusi sarake
(esim. koordinaatistomuunnos
, kun osoitetaan mekaanisen energian säilyminen heilurissa).
Nykyaikaiset taulukkolaskimet sisältävät hyvin laajan
valikoiman valmiita funktiota ja laskentamakroja.
Valikoimaan kannattaa tutustua käsikirjasta tai ohjelman
Help-toiminnon avulla, ettei suotta ala keksiä pyörää
uudelleen.
Uusien sarakkeiden laskeminen tapahtuu kirjoittamalla laskentakaava sarakkeen yhteen soluun ja kopioimalla se sitten muihin soluihin esim. kopioi-liitä -menetelmällä. Oletusarvoisesti kaavan rivi- ja sarakeviittaukset ovat suhteellisia, eli ne muuttuvat kopioinnissa automaattisesti rivin/sarakkeen suhteen. Jos kopioiduissa kaavoissa tarvitaan kaikissa lähtöarvona tiettyä vakiota, eli yhtä solua, tähän soluun viitataan absoluuttisella viitauksella, joka ei muutu kopioinnissa. Absoluuttinen viittaus osoitetaan $-merkillä.
Tarkastellaan
esimerkkiä, jossa on tutkitaan mekaanisen energian säilymistä
heilurin avulla. Pyritään osoittamaan riippuvuus
. Heiluri päästetään liikkeelle eri korkeuksilta,
ja mitataan aika, jonka heilurin punnus peittää radan
alimmassa kohdassa olevan valoportin. Siirretään korkeudet
ja ajat käsin taulukkolaskimeen, jossa lasketaan punnuksen
nopeudet ja nopeuden neliöt.
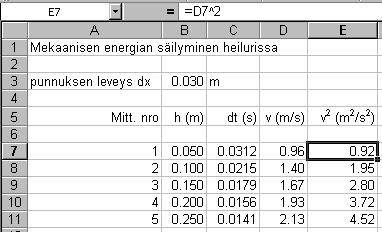
Kaavojen tulokset näkyvissä (normaali tila)
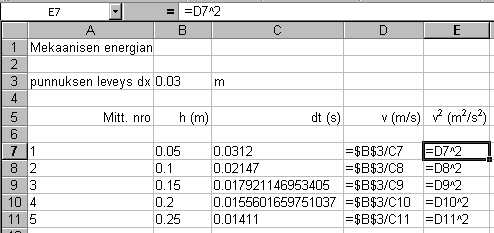
Kaavat näkyvissä.
Huomaa absoluuttiset viittaukset soluun B3,
sekä se että dt :n arvot on
siirretty
mittausohjelmasta kaikkine merkitsevine numeroineen.
Solujen tunnuksia käyttävät pitkät laskentakaavat voivat olla hankalasti hahmotettavia. Solujen tunnukset eivät myöskään ilmaise mitenkään, mikä merkitys ao. parametrilla kaavassa on. Näistä ongelmista päästään antamalla soluille tai laskenta-arkin alueille nimet. Suureiden arvoilla laskettaessa on luontevaa antaa nimet niin, että ne ovat joko samoja kuin käsiteltävien suureiden tunnukset, tai ainakin helposti yhdistettävissä suureiden tunnuksiin. Ylläolevaan heiluriesimerkkiin sovellettuna tämä tarkoittaa, että solulle B3 (punnuksen leveys) annetaan nimeksi dx, alueelle B7:B11 (heilurin maksimikorkeudet) annetaan nimeksi h_max, alue C7:C11 (valoportin ohitusajat) nimetään dt:ksi, ja alueelle D7:D11 (maksiminopeudet) annetaan nimeksi v_max. Nämä nimet ovat vain esimerkkejä: nimet voi valita vapaasti, kunhan ne eivät ole samoja kuin viittaukset soluihin tai sarakkeisiin.
LibreOfficessa solu tai alue nimetään valitsemalla se hiirellä, ja poimimalla valikosta Lisää - Nimet - Määritä. Nimettyyn alueeseen voidaan viitata kaavoissa suoraan nimellä. Viittaukset nimettyihin alueisiin ovat absoluuttisia, kuitenkin niin, että jos kaavassa on esim viittaus nimettyyn sarakealueeseen, kaava osaa poimia alueesta arvon samalta riviltä kuin millä kaava itse on. Katso alla oleva esimerkki.
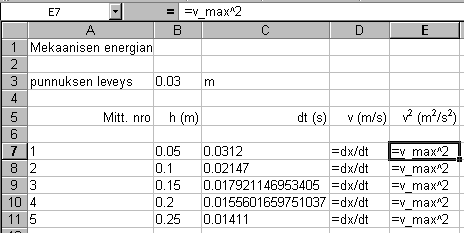
Kaavat näkyvissä, käytetty solujen ja alueiden nimeämistä.
Excelissä lukujen esitystarkkuutta muutetaan seuraavasti:
valitaan solu tai solut, joiden esitystarkkuutta halutaan muuttaa
ylävalikosta otetaan Muotoilu - Solut, ja Luku-välilehti
Luokka-listasta valitaan Luku, jos halutaan tavallinen desimaaliesitys, tai Tieteellinen , jos halutaan kymmenpotenssiesitys.
Desimaaliesityksessä haluttu desimaalimäärä säädetään Desimaaleja -asetuksella. Tieteellisessä esityksessä annetaan haluttu muotoilukoodi.
Kuvaajan piirtäminen tehdään hieman eri tavalla eri ohjelmissa. Käsitellään seuraavassa esimerkkinä, miten kuvaaja tehdään OpenOfficen versiolla 3.0.
Data, josta kuvaaja piirretään, on paras järjestää taulukkoon siten, että x-akselille tulevien arvojen sarake on vasemmalla, y-akselille tulevien arvojen sarake oikealla. Kuvaajan piirto aloitetaan valitsemalla hiirellä kuvaajaan tulevat sarakkeet. Jos valitaan sarakkeita jotka eivät ole rinnakkain, täytyy pitää Control-näppäintä alhaalla valintoja tehdessään.
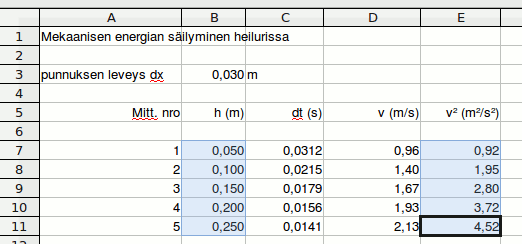
Solujen valinnaa jälkeen poimitaan valikosta Lisää - Kaavio, jolloin ohjattu kuvaajan luonti käynnistyy.
Ensin valitaan kaavion tyyppi. Useimmiten sopivin kuvaajatyyppi on XY-kuvaaja ilman pisteitä yhdistäviä janoja.
Seuraavaksi tarkistetaan tietoalue ja arvosarjat, niiden pitäisi olla valmiiksi oikein jos hiirellä valinta on tehty oikein.
Viimeiseksi asetetaan kaavioelementit. X- ja Y-akseleilla pitää olla otsikot (suureiden tunnukset ja yksiköt). Y-akselilta kannattaa yleensä ottaa ruudukon viivoitus pois. Samoin selite kannattaa yleensä ottaa pois.
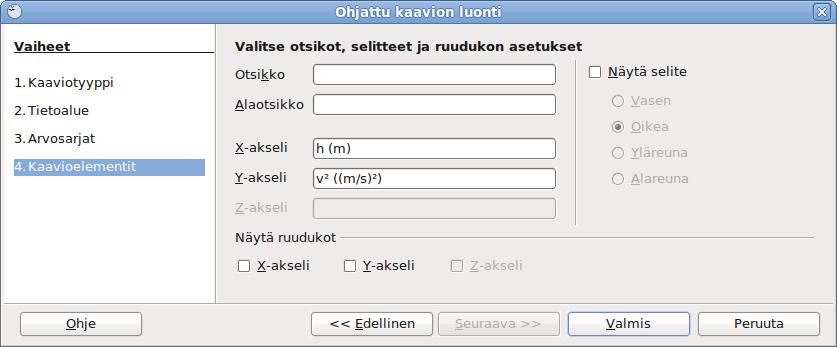
Saadaan ensimmäinen versio kuvaajasta. Siitä puuttuu vielä pisteisiin sovitettu suora. Asteikkojen esitystarkkuudet ovat peräisin taulukosta, ja hieman epätarkoituksenmukaiset.
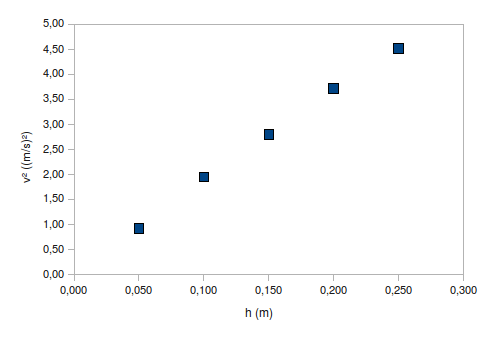
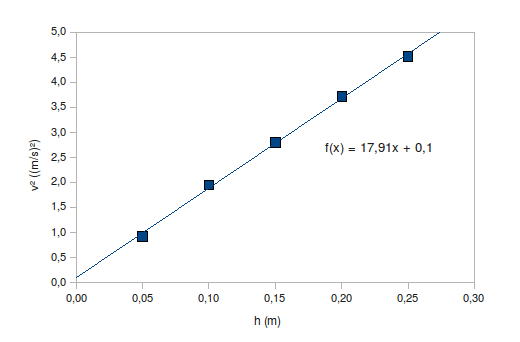
Pisteisiin sovitetaan suora seuraavasti.
Kaksoisklikataan kuvaajaa.
Klikataan oikealla napilla yhtä pistettä. Ponnahdusvalikosta valitaan Lisää trendiviiva.
Tyyppi -välilehdeltä valitaan regressiotyypiksi linearinen. Tarpeen mukaan valitaan Näytä yhtälö.
Viiva-välilehdellä voidaan tarpeen mukaan muuttaa viivan väriä, paksuutta jne.
Asteikkojen esitystarkkuudet muutetaan seuraavasti.
Kaksoisklikataan kuvaajaa.
Klikataan oikealla napilla haluttua akselia. Tässä pitää olla tarkkana. Ponnahdusvalikosta valitaan Objektin ominaisuudet.
Luku-välilehdellä otetaan ruksi pois kohdasta Lähdemuoto. Nyt numeroiden esitystapa ja -tarkkuus voidaan asettaa halutuksi.
Tarvittaessa Asteikko-välilehdellä voidaan asettaa akselin alku- ja loppupää sekä toisen akselin leikkauskohta.
Usein on tarvetta piirtää samaan koordinaatistoon useita kuvaajia. Tilanne on helppo silloin, kun kuvaajilla on samat X-akselin arvot. Tällöin valitaan yhdellä kertaa kaikki sarakkeet (X-sarake ja useita Y-sarakkeita), ja tehdään kuvaaja Chart Wizardin avustuksella kuten yllä.
Jos kuvaajissa on eri X-sarakkeet, täytyy käyttää toista menetelmää.
Valitaan hiirellä yhden kuvaajan X- ja Y-sarakkeet, ja aloitetaan kuvaajan piirtäminen ohjatun kaavion luonnin avulla kuten edellä.
Vaiheessa 3. Arvosarjat, klikataan Lisää.
Kohdassa Tietoalueet valitaan X-arvot. klikataan "Valitse tietoalue" -nappia, jolloin voidaan maalata taulukosta haluttu X-sarake. Vastaavasti valitaan Y-arvot ja maalataan Y-sarake.
Lisätään samalla tavalla kaikkien kuvaajien arvosarjat ja päätetään kuvaajan laatiminen kuten edellä.
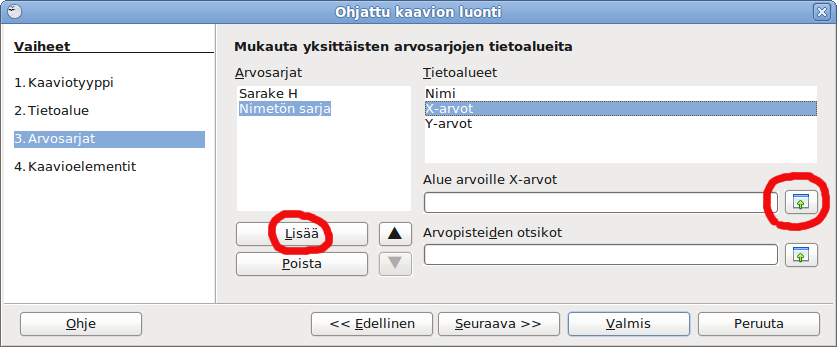
Näin piirrettyihin kuvaajiin voidaan vaikkapa sovittaa kuhunkin oma suoransa.
Kuten yllä on nähty, taulukkolaskimissa on mahdollisuus tehdä suoran (tai usean muunkin funktion) sovitus kuvaajan piirtämisen yhteydessä. Sinänsä kätevässä menetelmässä on pari heikkoutta. Sovituksen laskemiin kertoimiin ei voi viitata kaavoissa, eikä kertoimille lasketa virherajoja.
Yleiskäyttöisempi menetelmä on käyttää funktiota LINEST. Sen formaatti on
LINEST(DataY; DataX; LinearType; Stats)
Funktion käyttöä
kannattaa opiskella Helpistä. Katsotaan tässä
esimerkiksi suoran sovittaminen ylläolevan esimerkin
-pisteisiin. Lasketaan sovitusparametrit ja niiden virheet.
Maalataan sopivasta kohdasta laskenta-arkkia 2 x 2 solun alue funktion arvotaulukkoa varten.
Kirjoitetaan funktion syöttöriville =LINEST(E7:E11;B7:B11;1;1). Siis E7:E11 on y-muuttujan alue, B7:B11 on x-muuttujan alue. LinearType = 1 , jolloin suovitetun suoran vakiokerroin b lasketaan normaalisti (jos LinearType = 0 , suora pakotetaan kulkemaan origon kautta). Stats = 1 , jolloin lasketaan myös virhearviot.
Syötetään funktio laskenta-arkkiin taulukkofunktioksi painamalla Ctrl-Shift-Enter. Tällöin ohjelma laskee funktion arvotaulukon, joka näyttää seuraavalta:
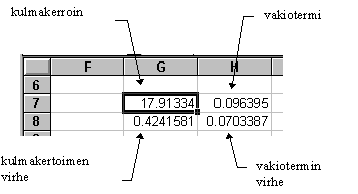
Siis sovitetun suoran
yhtälö tässä tapauksessa on
Parametrin "oikea" arvo on laskettujen virherajojen sisällä n. 68 % varmuudella, ja kaksinkertaisena otettujen virherajojen sisällä n. 95 % varmuudella.
Jos ei tarvita virhearviota, voi käyttää seuraavia yksinkertaisempia funktioita:
SLOPE(DataY; DataX) laskee sovitetun suoran kulmakertoimen
INTERCEPT(DataY; DataX) laskee sovitetun suoran yhtälön vakiotermin
Taulukkolaskimella voidaan luoda mallin pohjalta laskennallinen ennuste fysikaalisen systeemin käyttäytymisestä. Mallin siirtäminen ohjelman laskettavaksi on taulukkolaskinta käytettäessä helpompaa ja havainnollisempaa kuin perinteisillä ohjelmointikielillä.
Tutkitaan esimerkkinä
tilanteita, joissa halutaan ennustaa kappaleen rata, kun tunnetaan
massa ja ulkoinen kokonaisvoima. Jos voima ja massa ovat vakioita,
myös kiihtyvyys on vakio, ja radan ilmaisee yksiulotteisessa
tapauksessa yhtälö
. Tämä on helppo esittää taulukkolaskimella:
vakiot x0, v0
ja a ovat yksittäisiä soluja, ajan hetket t
sijoitetaan sarakkeeseen (voidaan ottaa käyttöön
apuvakio Dt, ja laskea ajan hetket
lisäämällä Dt
aina edelliseen t:n arvoon). x(t):n arvot
lasketaan omaan sarakkeeseensa yllä mainitulla kaavalla.
Jos voima ei ole vakio, tilanne on monimutkaisempi. Esimerkkitapauksia ovat putoamisliike väliaineessa (voima on Maan vetovoiman ja nopeudesta riippuvan väliaineen vastusvoiman summa), ja kitkattomalla vaakasuoralla alustalla jousen päässä värähtelevä punnus (voima on verrannollinen jousen venymään). Analyyttinen käsittely onnistuisi osassa muuttuvan voiman tapauksista lukion integraalilaskennan keinoin, osassa tarvittaisiin differentaaliyhtälöiden ratkaisemista. Taulukkolaskimella voidaan liikeyhtälö ratkaista numeerisesti, eli ennustaa kappaleen rata kun lähtöpaikka, alkunopeus, sekä voima ja sen riippuvuus (ajasta, nopeudesta tai paikasta) tunnetaan. Itse asiassa tällöin suoritetaan differentiaaliyhtälön numeerinen ratkaisu, mutta menetelmä on mahdollista ymmärtää ilman diffrentiaalilaskennan tuntemusta.
Menetelmässä
tutkittava aikaväli jaetaan lyhyisiin osiin. Alkuarvojen x0
ja v0 perusteella lasketaan
voima alkuhetkellä t0(jos voima riippuu
nopeudesta, lasketaan
; jos paikasta,
) ja lasketaan kiihtyvyys
. Koska aikaväli
on lyhyt, voidaan pitää kiihtyvyyttä tällä
välillä vakiona
. Näin ollen
ja
. Seuraavaksi lasketaan hetkellä t1
kappaleeseen kohdistuva voima F1, sitten
, jota pidetään vakiona välillä t2 - t1
j.n.e.
Tämä on Eulerin menetelmäksi kutsuttu tapa ratkaista differentiaaliyhtälö numeerisesti. On ymmärrettävää, että menetelmä aiheuttaa sitä suuremman virheen, mitä enemmän ja mitä karkeampia Δt-askelia otetaan. Tarkempia menetelmiä on olemassa, esim. Runge-Kutta -menetelmä, mutta siinä käytettäviä laskentakaavoja ei voi perustella yhtä yksinkertaisen fysikaalisesti kuin Eulerin menetelmässä.
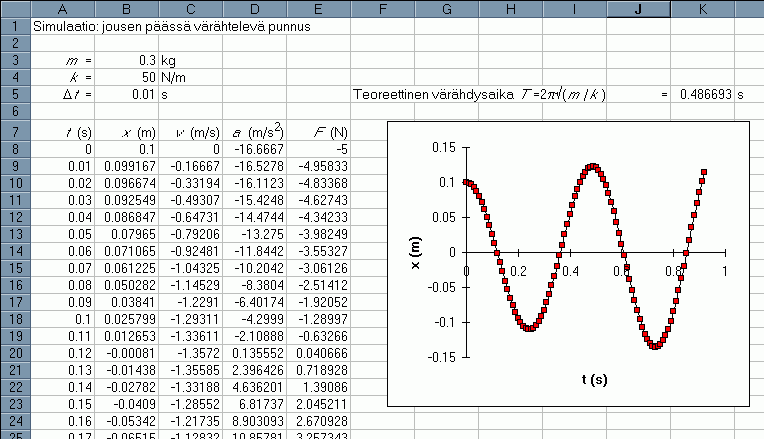
Voit imuroida tästä Excelillä tehdyn esimerkkisimulaation jousen päässä värähtelevästä punnuksesta: JOUSISIM.XLS .
Taulukkolaskimen käyttöä täytyy opiskella siinä missä muidenkin työkalujen. Tämän voi tehdä joko erikseen asiaan paneutuen, tai ohjelmalla tehtävän työn ohessa, sitä mukaa kun opeteltavia asioita tulee vastaan. Jälkimmäinen tapa voi olla stressaava, jos valmista pitäisi saada aikaan nopeasti, eikä aikaa opetteluun olisi.
Ohjelmien käsikirjat ovat nykyisin valitettavan suppeita, eikä opiskelija edes saa helposti käsiinsä yliopiston mikroverkon ohjelmien käsikirjoja. Käsikirjat on korvattu erilaisilla avustustoiminnoilla ja opetusohjelmilla. Tähän ei voi kuin sopeutua, ja opetella käyttämään näitä avusteita. Tai sitten täytyy ostaa erikseen jonkin "gurun" kirjoittama ohjekirja, joita kyllä yleisimmille ohjelmille löytyy, osalle jopa suomenkielisinä.
Ohjelmista kuitenkin pyritään tekemään helppokäyttöisiä, ja melko pitkälle pärjää jopa ilman opasteiden tutkimista, kun muistaa muutamat perustemput, joita standardien mukaan tehdyt ohjelmat nykyään tottelevat. Tärkein muistettava on se graafisten käyttöliittymien perusfilosofia, että ensin valitaan tekemisen kohteena oleva olio, sitten valitaan se mitä oliolle tehdään. Valikot yms. muuttavat sisältöään sen mukaan mikä olio on valittuna. Olio voi olla esim. kuvaajan akseli, jolla on ominaisuuksia: alku- ja loppupiste, tekstifontti, lukujen esitystarkkuus, jne. Hiiren kaksoisklikkauksella pääsee yleensä muokkaamaan valitun olion ominaisuuksia. Uusissa ohjelmissa hiiren oikeanpuolimmaisesta napista aukeaa paikallisvalikko, josta löytyvät ne temput jotka valitulle oliolle useimmiten halutaan tehdä.
Jari Lavosen Excel-opas: http://www.helsinki.fi/kasv/okl/malu/excel.html
De Jong, M. L. Computers in Introductory Physics. Computers in Physics, Vol. 5, No. 1, 1991. 12—15.
Kahaner D., Moler C., Nash S. Numerical Methods and Software. Prentice-Hall, 1989.
Misner, C. W. Spreadsheet physics. Reading, MA Addison-Wesley, 1991.
Potter, F., Peck, C. W., Barkley, D. S (editor). Dynamic Models in Physics. A Workbooks of Computer Simulations Using Electronic Spreadsheets. Volume One: Mechanics. Marina del Rey, 1989.
Webb, L. Spreadsheets in physics teaching. Phys. Educ., Vol. 28, No. 2, 1993. 77—82.