Main page
Department of Mathematics and Statistics
of University of Helsinki
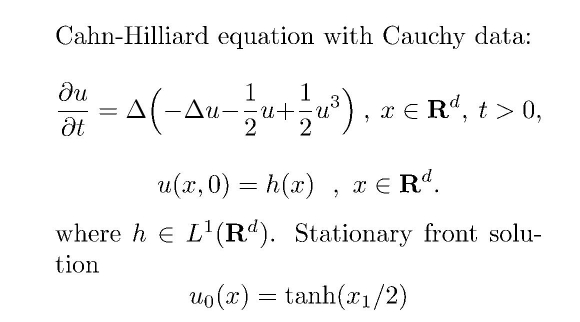
Formula 1. Cahn-Hilliard-equation.
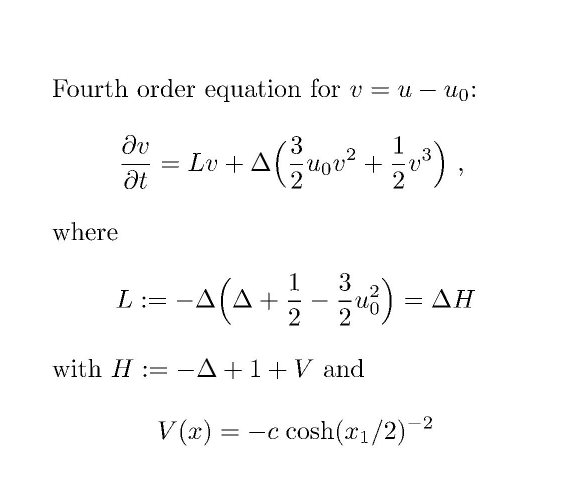
Formula 2. The parabolic equation for the perturbation.

|
The Cahn-Hilliard equation (Formula 1) can be used to model phase separation
in mixtures of two substances A and B: the function
u has values
in the interval [-1,1] with the endpoints describing the state
of pure phase of substance A, respectively, B. For a random
initial distribution h, numerical simulations show that
phase segregation evolves: domains of phase A and B start to
form. However, a rigorous mathematical analysis of this
phenomenon seems very difficult.
SOME RECENT ARTICLES
-
T.Korvola, A.Kupiainen, J.Taskinen:
Anomalous scaling for 3d Cahn-Hilliard fronts
Comm. Pure Appl. Math.
LVIII, (2005), 1077-1115.
This work deals with the simple situation that the initial
data is a perturbation of the stationary kink solution
tanh (x/2) for the unbounded Euclidean space of at least
dimension 3. We prove the stability: the function u tends,
as expected, to the stationary solution, if the initial
perturbation is small enough.
The method is based on a detailed spectral analysis
of the linear elliptic fourth order operator L, see Formula 2
(using the Melnikov, or Pego-Weinstein, method), and a fixed point argument
in some
properly chosen Banach spaces with weighted sup-norms.
-
J.Bricmont, A.Kupiainen, J.Taskinen:
Stability of Cahn-Hilliard fronts
Comm.Pure.Appl.Math. LII (1999), 839-871.
This earlier work proves the stability of the stationary solution
in the case x ∈ R. The approach is based on the
renormalization group method.
Back to main page .
|