Main page
Department of Mathematics and Statistics
of University of Helsinki

Formula 1. Linear water-wave problem.
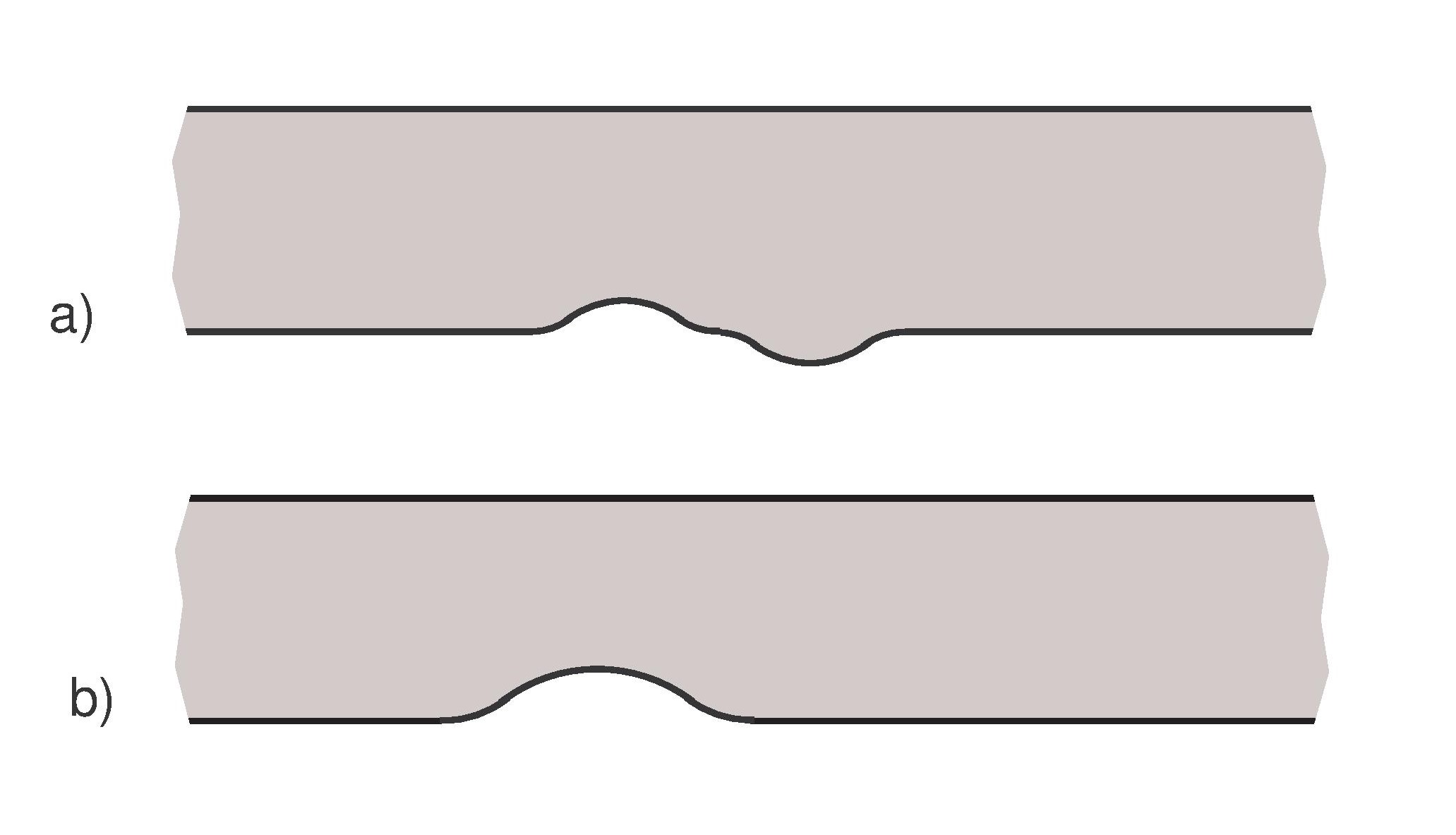
Figure 1. Water basin with possible invisible bottom shapes.
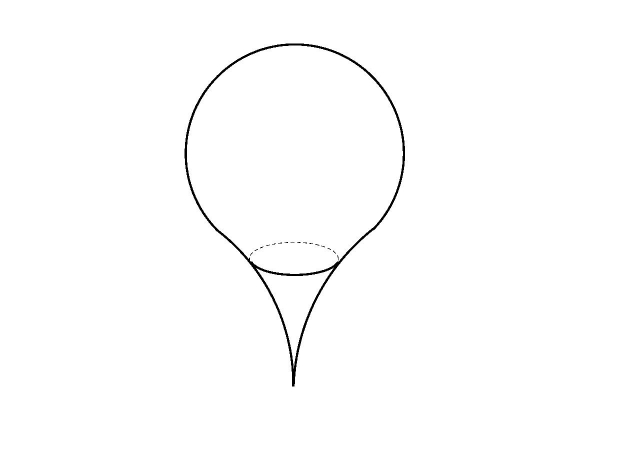
Figure 2. Domain with a cuspidal peak.
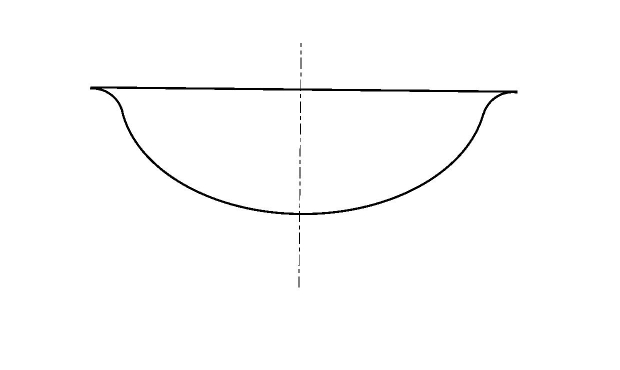
Figure 3. A water basin with cuspidal edge.
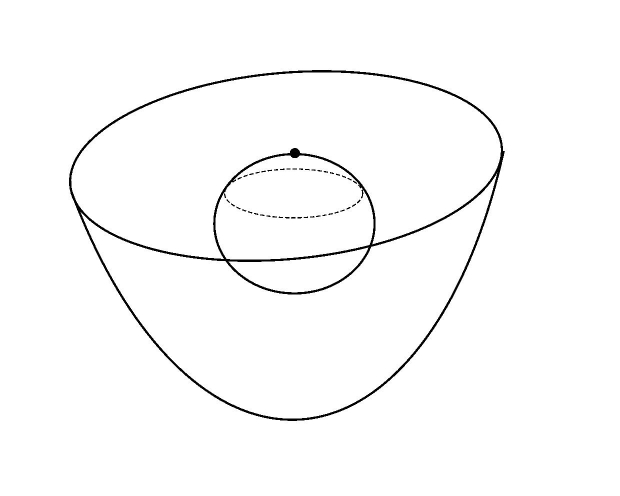
Figure 4. A water basin ("Loch Ness") with a submerged body ("monster").
|
We study problems with Steklov-type spectral conditions: the
spectal parameter appears in the boundary conditions. An example is the linear
water-wave problem, where the Steklov boundary condition appears on the free water surface; on
the bottom and walls of the water basin there are usual homogeneous
Neumann conditions.
In spite of the "unusual" boundary condition, it is possible to present a weak formulation
of this boundary problem such that standard Hilbert-Sobolev-space methods can be applied.
SOME RECENT ARTICLES
- S.A.Nazarov, J.Taskinen:
"Blinking eigenvalues" of the Steklov problem generate the continuous spectrum in a cuspidal domain.
Submitted..
We study the Steklov spectral problem
for the Laplace operator in a bounded domain D of dimension at least 2, with a
cusp such that the continuous spectrum of the problem is non-empty, and also in
a family of bounded domains D(r)
obtained from D by blunting the cusp at the distance of r > 0 from the cusp
tip. The spectrum in the blunted domain D(r) consists for a fixed r of an
unbounded positive sequence of eigenvalues, and we single out different types
of behavior of some eigenvalues as r tends to 0. In particular, stable,
"blinking", and "gliding" families of eigenvalues are found. We also describe a
mechanism which transforms the family of the eigenvalue sequences into the continuous spectrum of the problem in D, when r tends to 0.
Preprint .
- L.Chesnel, S.A.Nazarov, J.Taskinen:
Surface waves in a channel with thin tunnels and wells at the bottom: non-reflecting underwater topography.
To appear in Asymptotic Anal.
We consider the propagation of surface water waves in a straight planar channel
perturbed at the bottom by several thin curved tunnels and wells. We propose a
method to construct non reflecting underwater topographies of this type at an
arbitrary prescribed wave number. This is done by computing
asymptotic expansions of the diffraction solutions with respect to the small parameter of the geometry taking into account the existence of
boundary layer phenomena. We establish error estimates to validate the
expansions using techniques of weighted spaces with detached asymptotics. In
the process, we show the absence of trapped surface waves, if the
perturbations small enough.Theoretical and numerical examples are given.
Preprint .
- V.Chiado Piat, S.A.Nazarov, J.Taskinen:
Embedded eigenvalues for water-waves in a three
dimensional channel with a thin screen.
Quarterly J.Mech.Appl.Math. 71, 2 (2018), 187-220.
We construct asymptotic expansions as h ->0 for an eigenvalue embedded
into the continuous spectrum of water-wave problem in a cylindrical three dimensional channel
with a thin screen of thickness O(h). The screen may be either submerged or
surface-piercing. The channel and the screen are mirror symmetric so that imposing the
Dirichlet condition in the middle plane creates an artificial positive cut-off-value
M of the modified spectrum. The wetted part of the screen has a
sharp edge. Depending on a certain integral characteristics I of the screen profiles,
we find two types of asymptotics for the embedded eigenvalue, M - O(h^2) and
M - O(h^4) in the cases I> 0 and I=0, respectively.
We prove that in the case I<0 there are no embedded eigenvalues in the
interval [0, M], while this interval contains
exactly one eigenvalue, if M is non-negative. The main tools are the
reduction to an abstract spectral equation, mentioned above, and the use of the max-min-principle.
Preprint .
- S.A.Nazarov, J.Taskinen:
Radiation conditions for the linear water-wave
problem in periodic channels.
Math.Nachr.290, 11-12 (2017), 1753-1778.
We study the well-posedness of the linearized water-wave problem in a
periodic channel with fixed or freely floating compact bodies,
preprint
.
Posing proper radiation conditions requires a classification of incoming and outgoing waves.
This is done with the help of a certain skew-Hermitian form q, which
is closely related to the Umov-Poynting vector of energy transportation.
Our radiation conditions make the problem operator into a Fredholm operator of
index zero and provides the desired classification of
outgoing/incoming waves. They also lead to a novel, most natural properties and
interpretation of the scattering matrix, which becomes unitary and symmetric.
We use Floquet-Bloch-(or Gelfand-transform) techniques, leading to a generalized
spectral problem, where the dependence on the "spectral" parameter is quadratic
instead of linear. Floquet waves are defined as linear combinations of the
corresponding eigenvectors and their associated vectors belonging to the
Jordan chains. These are explicitly calculated in some typical cases.
- A.-S.Bonnet-BenDhia, S.A.Nazarov, J.Taskinen:
Underwater topography invisible for surface waves at given
frequencies
Wave Motion 57 (2015), 129-142.
We consider scattering of surface waves modeled by the linear water wave equation in
an unbounded two-dimensional domain of finite depth, at a given frequency and a given
incidence. Using asymptotic analysis for small perturbations of the bottom shape, we build
a fixed-point equation whose unique solution is a shape which cannot be detected by a
distant observer. Fig.1.
Here is a
preprint
.
- F.Bakharev, K.Ruotsalainen, J.Taskinen:
Spectral gaps for the linear surface wave model in periodic channels.
Quaterly J.Mech.Appl.Math. 67, 3 (2014), 343-362
We consider the linear water-wave problem in a periodic channel which consists of infinitely many identical containers
connected with apertures of width h. Motivated by applications to surface wave propagation phenomena,
we study the band-gap structure of the
continuous spectrum. We show that for small apertures there exists a large number of gaps and also find asymptotic formulas for the
position of the gaps as h-> 0 : the endpoints are determined within corrections of order
h^(3/2). The width of the first bands is shown to be O(h). Finally, we give a sufficient
condition which guarantees that the spectral bands do not degenerate into eigenvalues of infinite multiplicity.
Here is a
preprint
.
- J.Martin, S.A.Nazarov, J.Taskinen:
Spectrum of the linear water model for a two-layer liquid with cuspidal geometries at the interface
Z.Angew.Math.Mech. 1-18 (2014).
We show that the linear water wave problem in a bounded liquid domain may have continuous
spectrum, if the interface of a two-layer liquid
touches the basin walls at zero angle. The reason for this phenomenon
is the appearance of cuspidal geometries of the liquid phases.
We calculate the exact position of the continuous spectrum.
We also discuss the physical background
of wave propagation processes, which are enabled by the continuous spectrum.
Our approach and methods include constructions of a parametrix for the problem
operator and singular Weyl sequences.
Preprint
- S.A.Nazarov, J.Taskinen:
Properties of the Spectrum in the John Problem on a Freely Floating Submerged Body in a Finite Basin.
Differential Eq. 49, 12 (2013), 1544-1559.
We consider the problem of the interaction of surface waves with
a freely floating submerged body. In addition to the usual spectral Steklov problem
the problem contains a system of algebraic equations related to the motion of the
floating body. The spectral problem has quadratic dependence of the spectral
parameter, but it is converted into a standard
spectral equation for a self-adjoint operator in a certain Hilbert space.
In addition to general properties of the spectrum we investigate asymptotics
of eigenvalues and eigenvectors with respect to a small parameter (small deviation from a
fixed submerged body).
- J.Martin, J.Taskinen:
Linear water-wave probelm in a pond with a shallow beach.
Applicable Anal. 92, 10 (2013), 2229-2240.
This is continuation to the paper in Math.Scand 106. We solve
some cases left open in the citation, in particular we show
under weaker geometric assumptions that the essential spectrum is
still nonempty. Of course, these results concern cases where the
sharpness exponent, describing the depth of the shallow water basin,
is large enough.
Preprint
- S.A.Nazarov, J.Taskinen:
Localization estimates for eigenfrequences of waves trapped by freely floating body in channel.
SIAM J.Math.Anal. 45, 4(2013), 2523-2545.
We study the linear water-wave problem in the case of a
freely floating body in an unbounded cylindrical channel.
The aim is to find trapped modes, which correspond
to eigenvalues outside the continuous spectrum (once the
problem is formulated as a standard spectral problem for a
bounded linear operator in a suitable Sobolev-type Hilbert
space).
We derive a suitable reference problem involving a boundary condition
on the wetted surface of the body. Sufficient
conditions for the existence of trapped modes are found
for the reference problem and then, using a localization estimate, for
the original problem. Applications of these conditions
to concrete cases are given.
Preprint
- S.A.Nazarov, J.Taskinen:
Two-sided estimates for eigenfrequencies in the John problem on freely
floating body.
J. Math.Sci 185,1 (2012), 50-63. Translated from: Zapiski Nauchnykh
Seminarov POMI 397 (2011), 89-114.
The two-dimensional problem on oblique incident
waves and a freely floating cylinder is reduced to the
study of the
spectrum of a suitable self-adjoint operator in Hilbert space.
Using tools from
spectral measure theory we estimate the difference between
eigenfrequencies of the original problem and
a problem on an
inert body, which does not react to the buoyancy forces. We give
the localization of eigenfrequencies of the freely
floating body, and in addition derive a sufficient condition for the
existence of the point
spectrum in the corresponding boundary value problem.
Preprint
- S.A.Nazarov, J.Taskinen, J.Videman:
Asymptotic behaviour of interfacial trapped modes in a two-layer fluid.
Wave Motion 50,2 (2013), 111-126.
The setting here is a liquid with two layers having different densities,
for example unmixed layers of sweet and salinated water. In addition,
there is a fixed horizontal cylindrical obstacle, which may or may
not pierce the free liquid surface or the interface.
We present a sufficient condition for trapped modes (see above)
of water-waves hitting the obstacle obliquely, especially in the
case when the density difference between the fluid layers is
small. By examining a suitable auxiliary problem which corresponds to the
limit case when the density difference ε tends to zero,
we derive
an asymptotic formula for the interfacial trapped mode frequency and establish
a condition guaranteeing the existence of trapped modes for small values of
ε.
-
S.A.Nazarov, J.Taskinen:
Radiation conditions at the top of a rotational cusp in
the theory of water-waves.
Math.Model.Numer.Anal. 45,4 (2011), 947-979.
We study the linearized water-wave problem in cuspidal domains
like in Fig.4, denoting the contact point of the submerged body with the
water surface by O. The solution operator of the problem is not
of Fredholm index 0 in the usual function spaces. To make it
have this property, it is necessary to distinguish the spaces of
incoming and outgoing waves (seen from the point O),
and pose radiation conditions to define the proper domain for solution
operator. The spaces of incoming and outgoing waves are found
by deriving a limit ODE via asymptotic analysis. We discuss the connection
of the radiation conditions to the Mandelstam principle.
-
S.A.Nazarov, J.Taskinen:
On the spectrum of the Steklov problem in a domain
with a peak.
Vestnik St. Petersburg Univ. 41, 4 (2008), 56--65.
We study the Steklov spectral problem for the Laplacian; this is similar to
the water-wave problem of Formula 1, except that the spectral boundary
condition (last line) is valid a.e. on the boundary. The domain is
cuspidal, like in Fig.2. Again, the geometry of the domain is described
by a sharpness exponent γ > 0 of the peak. We show that if
γ < 1, then the spectrum is discrete and contained in the positive
real axis. In the case γ = 1 there is a number r > 0 such that
the discrete part of the spectrum is contained in the interval (0,r) and
moreover the semi-axis [r, ∞) forms the continuous spectrum.
In case γ > 1 the point 0 belongs to the continuous spectrum.
- S.A.Nazarov, J.Taskinen:
On essential and continuous spectra of the
linearized water--wave problem in a finite pond.
Math. Scand. 106, 1 (2010), 141-160.
We study the linearized water-wave problem (Formula 1) on domains with
cuspidal edges or rotational cusps (Fig. 3 and 4). The results on the spectrum
are similar to those in the above paper, but for large sharpness
indices the complete structure of the spectrum remains as an open problem.
Back to main page .
|