Main page
Department of Mathematics and Statistics
of University of Helsinki
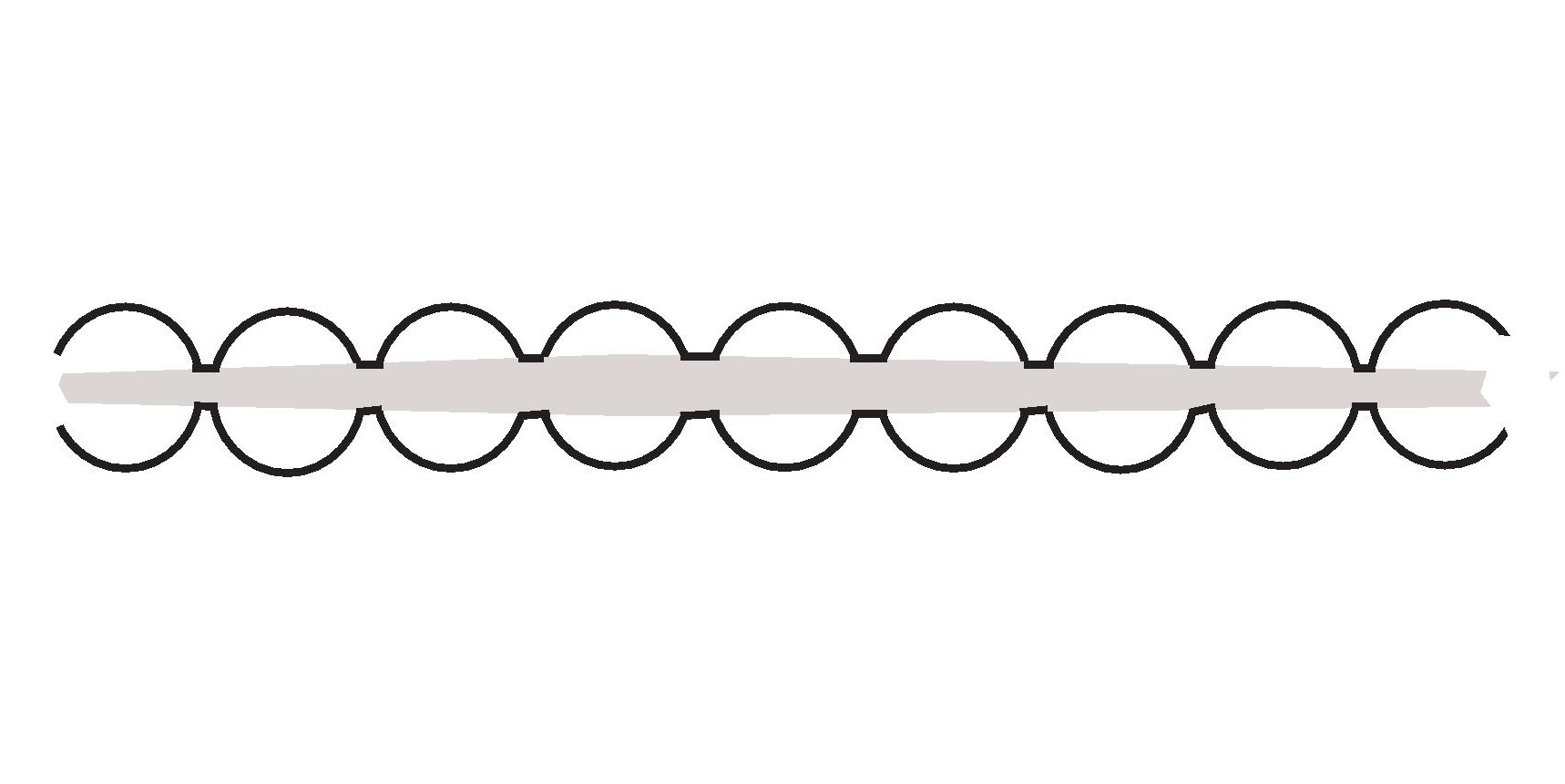
Fig.1. Thinning ligaments.
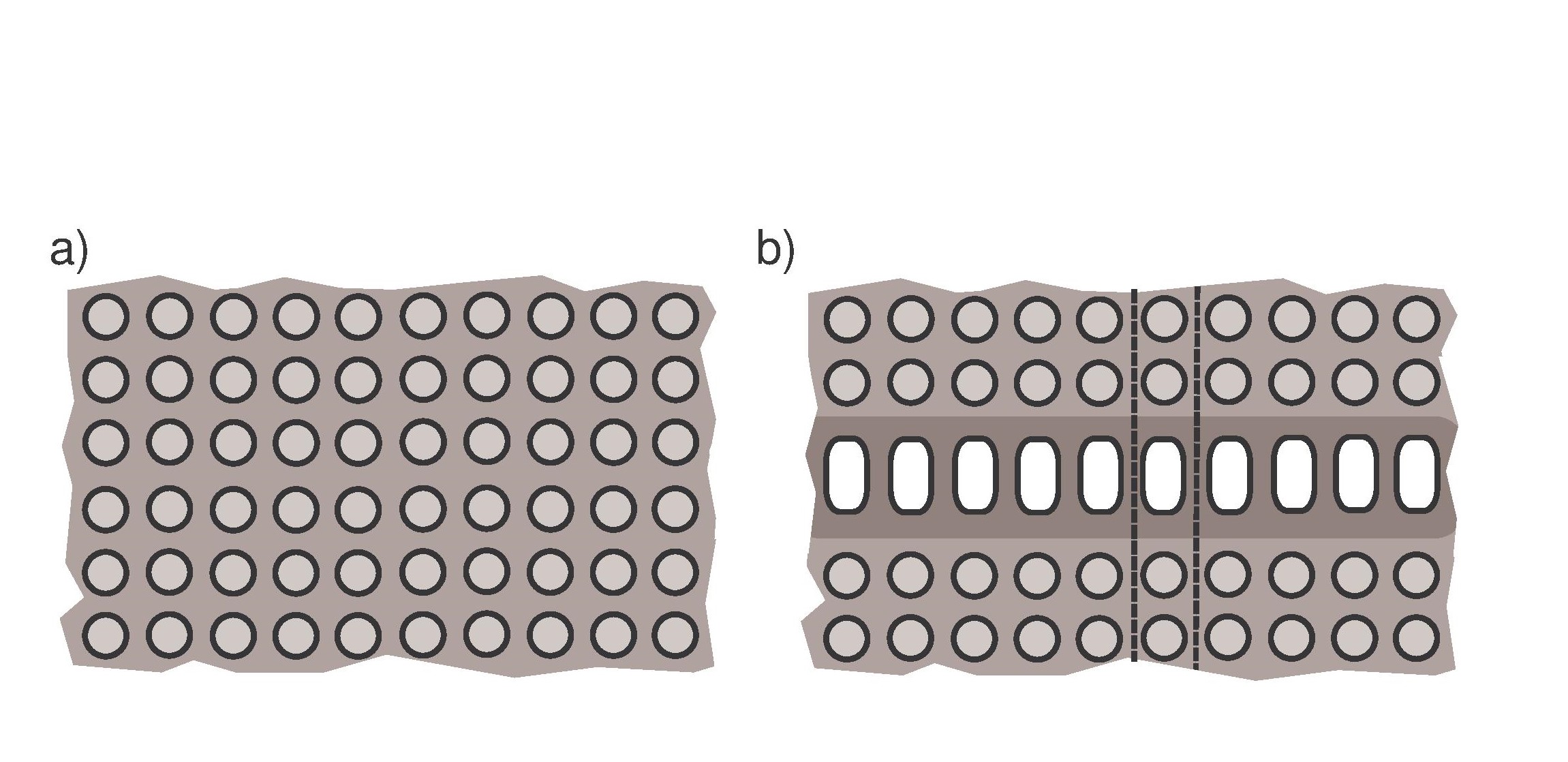
Fig.2. Perforated plane, noncompact perturbation.
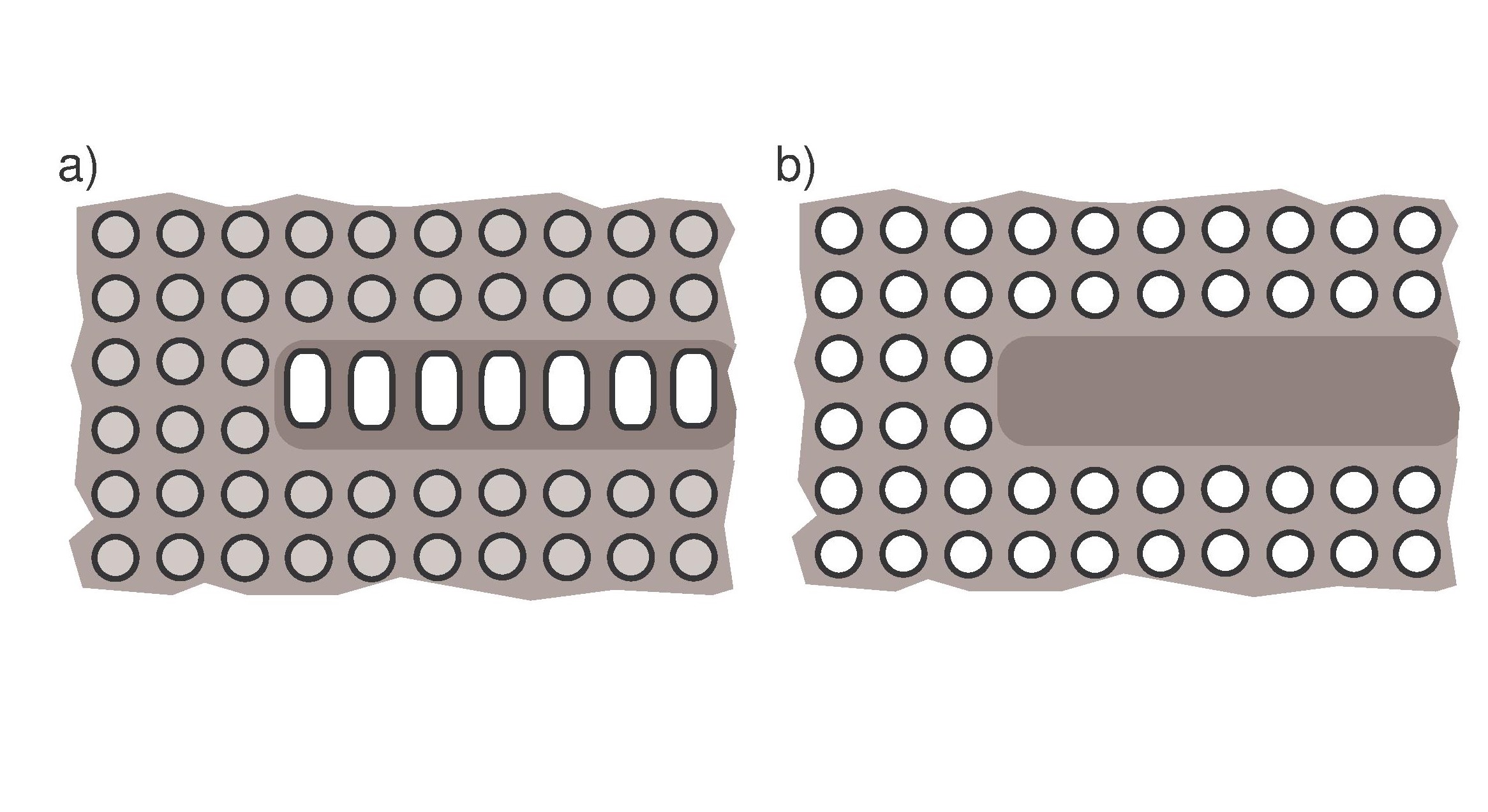
Fig.3. Open waveguides.
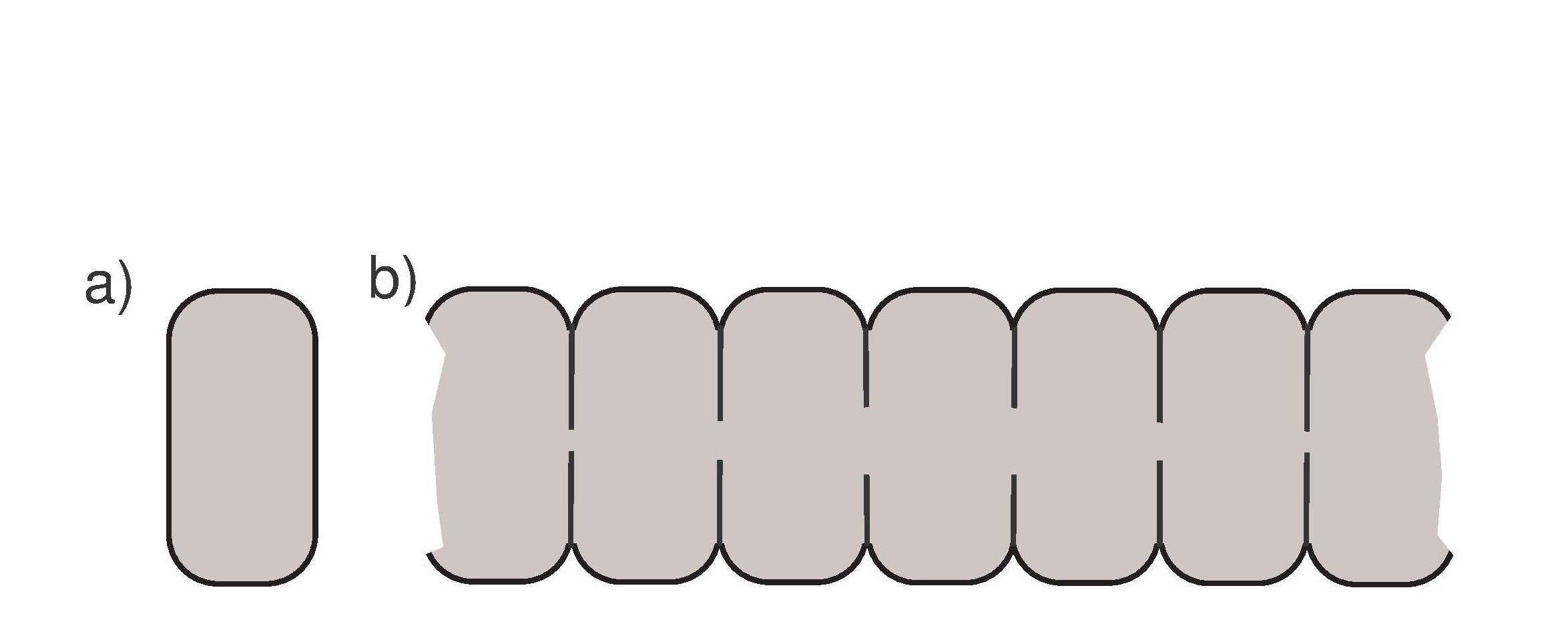
Fig.4. Narrowing apertures.
|
The questions being investigated concern gaps of the essential spectra in periodic domains, non-compact perturbations of domains and resulting perturbations
of essential spectra, Dirichlet-Laplace eigenfunctions and their dependence on the geometry of the domain, effects of boundary singularities (cusps) to the
spectrum, thin structures of domains and so on. We mostly study problems with Neumann boundary conditions, but as already mentioned, Dirichlet and also
Robin conditions appear here. For Steklov conditions there is a different page.
SOME RECENT ARTICLES
-
V.Kozlov, J.Taskinen:
Floquet problem and center manifold reduction for ordinary differential
operators with periodic coefficients in Hilbert spaces.
To appear.
We consider first order differential equations with operator
coefficients depending periodically on a variable t belonging to the
real line, the operators acting in a pair of Hilbert spaces. Our results
generalize the approach of the first author and V.Mazya, presented in their
book Differential equations with operator
coefficients with applications to boundary value problems for partial
differential equations (Springer, 1999), which deals with the case of
perturbations of constant operator coefficients.
Our setting models both elliptic equations with periodic coefficients in a
cylinder and parabolic equations with time periodic coefficients. The aim
is to split the system into a finite dimensional system of ordinary
differential equations with constant coefficients and an infinite dimensional
part whose solutions have better properties in the sense of a faster
decay at the infinity. The result complements the well-known asymptotic
results for periodic hypoelliptic problems in cylinders
and for elliptic problems in quasicylinders, see S.A.Nazarov, Elliptic boundary value problems with periodic coefficients in a cylinder,
Izv. Akad. Nauk SSSR Ser. Mat. 45 (1981).
The goal is achieved by constructing a projection operator
which is defined pointwise with respect to the variable t, and which
a bit unexpectedly commutes with the spectral projections. We work within the
general theory of analytic Fredholm families as in
P.Kuchment, Floquet theory for partial differential equations, Birkhauser (1993).
As an application we give a center manifold reduction for a class of non-linear
ordinary differential equations in Hilbert spaces with periodic coefficients. This
result generalizes the known case with constant coefficients, see
for example A. Mielke, Hamiltonian and Lagrangian flows on center
manifolds, Springer Lecture Notes in Mathematics vol. 1489 (1991).
Here is a
preprint.
-
S.A.Nazarov, J.Taskinen:
Essential spectrum of periodic medium with sparsely placed foreign
inclusions.
To appear in Pure Appl. Functional Anal.
We study the essential spectrum of a formally self-adjoint
system of partial differential equations, for example the elasticity system,
in periodic domains with non-periodic perturbations. The perturbation
is realized as a sparse distribution of identical foreign cells in a periodic
medium in R^d, d > 1 . It is shown that the essential spectrum consists of
the essential spectrum, with band-gap structure, of the corresponding
problem in the purely periodic medium and of the discrete spectrum of
the model problem, where the periodicity is broken by one foreign cell
only. The increment of the essential spectrum, caused by the perturbation, may occur either inside the spectral gaps, or below the spectrum
of the unperturbed problem.
The work generalizes the results of our paper in J.M.A.A (2018).
Several aspects require new proofs, for example the exponential decay of the
solutions of the model problem.
Preprint.
-
S.A.Nazarov, N.Popoff, J.Taskinen:
Plummeting and blinking eigenvalues of the Robin Laplacian in a cuspidal domain. To appear in Proc. Royal Soc. Edinburgh Sect. A Mathematics.
This paper contains a study of the Robin Laplacian in the domains D and
D(r) with a sharp cusp and, respectively, a cusp blunted at the distance
r > 0
of the peak tip. If the Robin coefficient is large enough, the spectrum of
the problem in D is known to be residual and
to cover the whole complex plane, but on the contrary, the spectrum in the
Lipschitz domain D(r) is discrete. We study the
behavior of the discrete spectrum as the blunting parameter r tends to 0
and reveal some strange asymptotic behavior. In particular we
construct "hardly movable" and "plummeting" families of eigenvalues.
The first type of the eigenvalues do not leave a small neighborhood of
a point for any small r > 0 while the second ones move at, in some sense,
high speed downwards along the real axis to the negative infinity as
r decreases
(the problem on D does not correspond to a positive operator!). Also, any point of the real
axis is a "blinking eigenvalue", i.e., it belongs to the spectrum of the
problem in D(r) almost periodically in the log r scale.
The techniques involve dimension reduction and self-adjoint
extensions, in addition to more standard Hilbert-Sobolev space
operator theory.
Preprint.
-
S.A.Nazarov, J.Taskinen:
Essential spectrum of a periodic waveguide with non-periodic
perturbation. J.Math.Anal.Appl.463 (2018), 922-933
We consider the spectral Dirichlet-Laplace problem on a domain which is formed from a periodic domain
G perturbed by non-compact, nonperiodic changes of geometry. We show that the domain perturbation causes an
addition to the essential spectrum, which consists of isolated points belonging to
the discrete spectrum of a model problem. This model problem is posed on a
domain, which is just a compact perturbation of G. We discuss the position of
the new spectral components in relation to the essential spectrum of the problem in the domain G.
Here is a
preprint.
-
S.A.Nazarov, J.Taskinen:
Singularities at the contact point of two kissing Neumann balls.
J.Differential Eq. 264, 3 (2018), 1521-1549.
We investigate eigenfunctions of the Neumann Laplacian in a bounded domain D contained in Rⁿ, n > 1,
where a cuspidal singularity is caused by a cavity consisting of
two touching balls, or discs in the planar case. We prove that the eigenfunctions
with all of their derivatives are bounded in the closure of D, if the dimension n=2,
but in dimension n > 2 their gradients have a strong singularity which can be as large as of order
|x -O|^(- 2 + √2) at the point of tangency O.
Here is a
preprint.
-
S.A.Nazarov, J.Taskinen:
Pathology of essential spectra of elliptic problems in periodic family of beads threaded by a spoke thinning at infinity.
Submitted.
We construct unbounded domains, which are nearly periodic waveguides,
such that a large class of elliptic spectral problems have essential spectra with infinitely
many spectral gaps. The domains consist of infinitely many identical translates of a bounded
periodicity cell, connected by a spoke thinning at inifinity, see Fig.1. Here is a
preprint.
-
F.Bakharev, G.Cardone, S.A.Nazarov, J.Taskinen:
Effects of Rayleigh waves to essential spectra
in composite periodic plane.
Integral Eq.Oper.Theory 88 (2017), 373--386.
We give an example of a scalar second order differential operator in the plane
with double periodic coefficients and describe its modification, which causes
an additional spectral band. The modified operator acts in the composite
plane and it is obtained by applying to the coefficients a mirror reflection with
respect to a vertical or horizontal line. This change gives rise to Rayleigh
type waves localized near the line.
-
G.Cardone, S.A.Nazarov, J.Taskinen:
Spectra of open waveguides in periodic media.
J. Functional Anal. 269 (2015), 2328-2364.
We study the essential spectra of some elliptic systems on
doubly periodic planar domains perturbed by non-compact perturbations, for example
by an infinite row of identical translated discs, see Fig.2,3.
A non-compact perturbation may change the essential spectrum, contrary to
a compact perturbation. We show that
the essential spectrum of the problem consists of the essential spectrum of
the purely periodic problem and another component, which is the union of the
discrete spectra of model problems (related to the perturbation) in the infinite perturbation strip.
Here is a
preprint.
-
S.A.Nazarov, E.Pérez, J.Taskinen:
Localization effect for Dirichlet eigenfunctions in thin non-smooth domains.
Transactions A.M.S. 368 (2016), 4787-4829.
We study the localization effect for the eigenfunctions of the Laplace-Dirichlet problem
in a thin three-dimensional plate with curved non-smooth
bases. We show that the eigenfunctions are localized at the thickest
region, or the longest traverse axis, of the plate and that
the magnitude of the eigenfunctions decays exponentially as a function of the distance to
this axis.
The results imply the existence of
gaps in the essential spectrum of the Dirichlet Laplacian in a related
unbounded double-periodic domain.
Here is a
preprint.
-
F.Ferraresso, J.Taskinen:
Singular perturbation Dirichlet problem in a double-periodic perforated plane.
To appear in Annali Univ.Ferrara
This is a generalization of the paper in J.Math.Sci 2012, below.
Here is a
preprint.
-
S.A.Nazarov, J.Taskinen:
Structure of the Spectrum of a Periodic Family of Identical Cells Connected by Converging Apertures.
J.Math.Sci. 194,1 (2013), 72-82.
We construct a waveguide where the essential spectrum of the Laplace-Dirichlet problem consists of
a countable set of points in the real positive semi-axis and thus has infinitely many gaps.
The waveguide is build from a family of identical cells, which are connected by apertures in their
common walls; the sizes of the apertures decrease when the distance to the
origin increases, see Fig.4. It is shown that the lowest point of the
essential spectrum is the limit of an infinite sequence of eigenvalues in the discrete spectrum.
We formulate a hypothesis on the structure
of the discrete spectrum inside gaps and present some unsolved problems.
-
S.A.Nazarov, J.Taskinen:
Spectral Anomalies of the Robin Laplacian in Non-Lipschitz Domains.
J.Math.Sci.Univ.Tokyo 20, 1 (2013), 27-90.
We consider the spectral Laplace-Robin problem in bounded peak shaped domains
of Rⁿ, n > 1. In case of a sufficiently sharp peak and
"wrong" sign of the Robin coefficients, the spectrum becomes pathological:
the residual spectrum covers the whole complex plane, while all
complex numbers are eigenvalues of the adjoint problem operator.
Our results solve a spectral problem
posed by H. Amann and D. Daners.
-
S.A.Nazarov, K.Ruotsalainen, J.Taskinen:
Spectral gaps in the Dirichlet and Neumann problems on the plane perforated
by a double-periodic family of circular holes.
J.Math.Sci. 181,2 (2012), 164-222.
We study spectral Laplace problem with Dirichlet or Neumann boundary
conditions on the following domain: it is the plane perforated by
a symmetric lattice of discs such that the coordinates of their center
points are integers and the radii are equal to R ∈ (0,1/2) .
If R were equal 1/2, the problem would reduce to a
standard problem in a bounded domain having discrete spectrum. On the
other hand, for very small R the spectrum has the properties
typical for unbounded domains; it may conincide with a half ray
[a, ∞) of the positive real axis.
In this work we prove the appearance of gaps in the essential spectrum,
when R starts to diminish from the value 1/2. Moreover,
we show that any prescribed number of gaps appear, if R is chosen
suitably.
-
S.A.Nazarov, K.Ruotsalainen, J.Taskinen:
Gaps in the spectrum of the Neumann problem on a perforated
plane.
Dokl.Math. 86,1 (2012), 1-5.
This is related to the J.Math.Sci 2012 -paper.
-
S.A.Nazarov, J.Taskinen:
On the spectrum of the Robin problem in a domain with a peak.
Funct.Anal.Appl. 45,1 (2011), 93-96.
We study the spectral Laplace problem endowed with the Robin boundary
conditions in a non-smooth, peak-shaped bounded domain, and give an example
of a case where the spectrum is pathological: the residual spectrum fills
the whole complex plane. This is a consequence of the fact that the
quadratic form associated to the problem operator is not semi-bounded
(in the sense of Birman-Krein-Vishik theory). Full details of proofs
are in the long J.Math.Sci.Univ.Tokyo-paper in 2013.
- S.A.Nazarov, J.Sokolowski, J.Taskinen:
Neumann Laplacian on a domain with tangential components in the
boundary.
Ann.Acad.Sci.Fenn. 34,1 (2009), 131-143.
We study the Neumann problem for the Poisson equation in a domain
Ω ⊂ Rⁿ
where two boundary components are tangential at a single point,
so that a rotational cusp is formed. An example is formed by
two tangential balls. The main problem is to find our
whether solutions with bounded energy, or finite Dirichlet integral, exist.
We show that this is true if and only if
where γ is
a geometric parameter describing the sharpness of the cusp. (In a
simple example, the contact point could be the origin of R³
and the domain could consist in a neighbourhood of 0
of the points x= (y,z) where y ∈ R²
and z is bounded between 0 and 1 + γ :th
power of |y|.
In the
situation of Fig. 1 and 2 we have γ = 1, so bounded energy
solutions exist.)
-
G.Cardone, S.A.Nazarov, J.Sokolowski, J.Taskinen:
On asymptotics of Neumann harmonics when a cavity is close
to the exterior boundary of the domain.
C.R.A.S. Mecanique 335 (2007), 763-767.
This is an introduction to the previous paper.
-
S.A.Nazarov, J.Taskinen:
Asymptotics of the solution to the Neumann
problem in a thin domain with sharp edge.
J.Math.Sci. 142,6 (2007), 2630-2644. Russian original:
Zapiski Nauchnyh Seminarov POMI 332 (2006), 193-219.
The domains Ω ⊂ R³
considered in this work have a cuspidal edge - as a model think about
a filled saucer or plate. In addition, the domain depends on a
small parameter h: the thickness or height of the plate Ω
is proportional to h. We consider the Neumann problem for elliptic
second-order operators in Ω, for the unknown function u.
We derive a degenerate limit equation for h → 0, find its solution
U, and show that for a suitable Sobolev H¹ -norm,
the asymptotic error estimate
|| u - U|| = O(√h) holds.
Back to main page .
|