Main page
Department of Mathematics and Statistics
of University of Helsinki
Figure 1. Waveguides.
Figure 2. Waveguides.
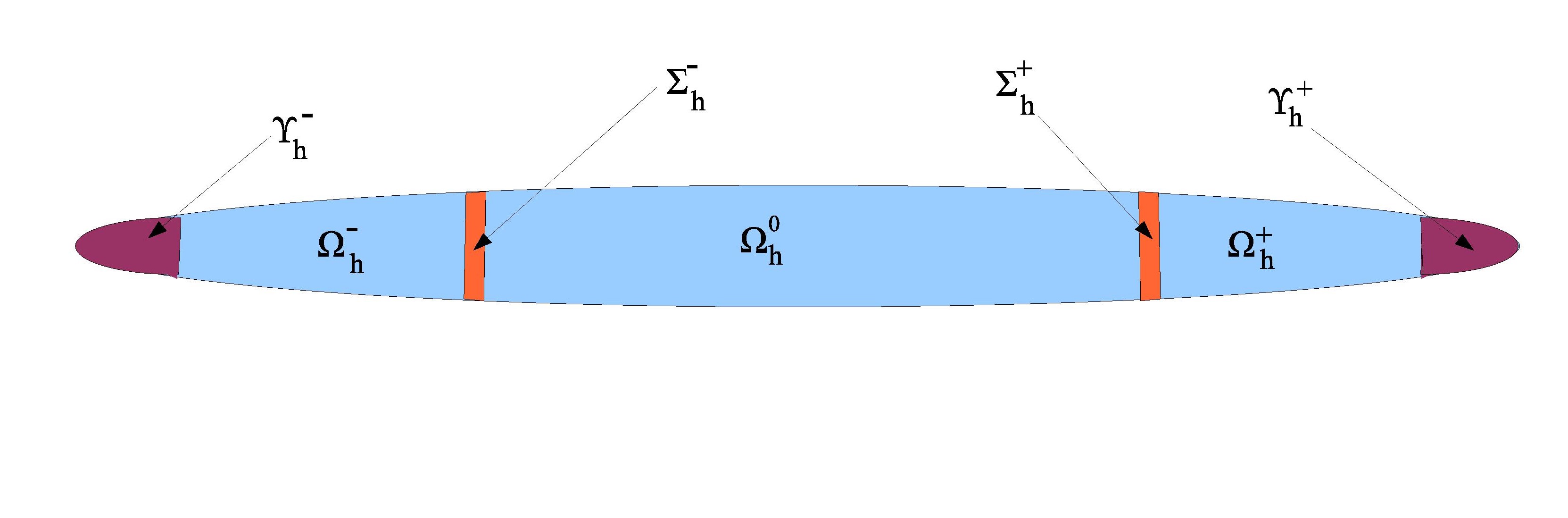
Figure 3. Thin rod with rounded edges.
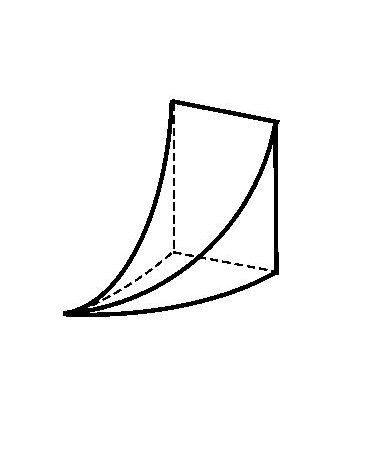
Figure 4. Domain of beak shape.
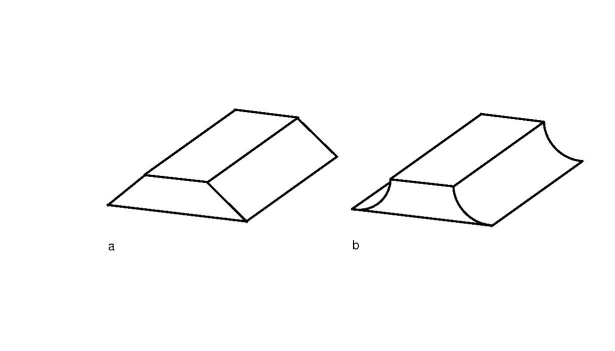
Figure 5. Corner and cuspidal domains.
|
We study the linear spectral elasticity and piezoelectricity problems. In the case of unbounded domains (waveguides) the main results concern
gaps in the essential spectra. Other results include existence of essential spectrum in the case of some cuspidal bounded domains.
SOME RECENT ARTICLES
-
G.Leugering, S.A.Nazarov, A.S.Slutskij, J.Taskinen:
Asymptotic analysis of a bit brace shaped junction of thin rods.
To appear in Z. Angew. Math. Mech ZAMM
We present a 1-D model of a junction of five thin elastic rods forming the shape of a bit brace
(hand drill), or, a crankshaft. The distinguishing feature of this junction is the existence of the so called movable elements, which are rods and knots requiring modifications of the classical asymptotic
ansatze. These consist of constant longitudinal displacements on the edges of the skeleton of the
junction and affect the transmission conditions at its nodes. We provide asymptotic formulas for the
displacements, stresses and elastic energy, as well as error estimates. An exact solution of the model
is given for a particular loading.
Preprint.
-
G.Leugering, S.A.Nazarov, J.Taskinen:
Umov-Poynting-Mandelstam radiation conditions in periodic composite piezoelectric waveguides.
Asymptotic Anal. 111, 2 (2019), 69-111.
We develop and investigate radiation conditions at infinity for the linear piezoelectricity problem
in unbounded periodic domains. The approach is based on the Mandelstam radiation principle according
to which the energy flux at infinity is directed away from the source. We discuss the special cases,
where the more conventional radiation conditions fail, and provide examples containing purely elastic insulating
and conducting inclusions as well as special cases of purely elastic and acoustic waveguides.
Here is a
preprint.
-
F.L.Bakharev, J.Taskinen:
Bands in the spectrum of a periodic elastic waveguide.
Zeitschrift Angew.Math.Phys. 68 (2017).
We study the spectral linear elasticity problem in an unbounded periodic waveguide, which consists of a sequence of identical bounded
cells connected by thin ligaments of diameter of order h >0. The essential spectrum of the problem is known to have band-gap structure.
We derive asymptotic formulas for the position of the spectral bands and gaps, as h approaches 0, so the method is different from some of our other papers,
where max-min-principle is applied; for example the Applicable Analysis-paper, 2010. In both cases, approximate eigenfunctions are
constructed, but in connection with the max-min-principle, they are formed by more straightforward ways by using cut-off functions
related to the geometry of the domain,
whereas in the present paper the asymptotic representation is by far more involved and also
leads to more accurate results. In particular we have a sufficient condition which guarantees that a spectral band does not degenerate into
an eigenvalue of infinite multiplicity.
Here is a
preprint.
-
S.A.Nazarov, J.Taskinen:
Elastic and piezoelectric waveguides may have infinite number of gaps in their spectra.
Comptes Rendus Mécanique. 344 (2016), 190--194.
We consider elastic and piezoelectric waveguides composed from identical
beads threaded periodically along a spoke converging at infinity.
We show that the essential spectrum constitutes a non-negative
monotone unbounded sequence and thus has infinitely many spectral gaps.
Here is a
preprint.
-
S.A.Nazarov, J.Taskinen:
Spectral gaps for periodic piezoelectric waveguides.
Zeitschrift Angew.Math.Phys. 66 (2015), 3017-3047
We construct a family of periodic piezoelectric waveguides
depending on a small geometric parameter h > 0 , with the following property:
as h -> 0 , the number of gaps in the essential spectrum of the
piezoelectricity problem grows unboundedly.
The method is similar to that in the Applicable Analysis 2010-paper, but there is a major technical complication
caused by the a priori non-seldadjointness of the piezoelectricty problem. We use a self-adjoint reduction scheme
developed earlier by S.Nazarov. However, this leads to a new non-local term in the reduced elliptic self ajoint
boundary problem. This complicates the use of the max-min-principle, but it turns out possible to derive the
needed estimates by using suitable Hardy-type inequalities and proper, special weighted Sobolev norms, among other things.
Here is a
preprint.
-
S.A.Nazarov, A.S.Slutskij, J.Taskinen:
Korn inequality for a thin rod with rounded ends.
Math.Methods Appl.Sci. 37, 16 (2014), 2463-2483
We consider an elastic rod (Fig.3) with rounded ends and diameter proportional to a small parameter h >0
The roundness of the ends is described by an exponent 0 < m < 1 . We derive for the rod an asymptotically sharp Korn
inequality with a special weighted anisotropic norm. Weight factors with m-dependent powers of h appear both
in the anisotropic norm and the Korn inequality itself, and we discover three
critical values m = 1/4, m=1/2 and m=3/4 at which these exponents are crucially changed.
-
S.A.Nazarov, K.Ruotsalainen, J.Taskinen:
Essential spectrum of a periodic elastic waveguide may
contain arbitrarily many gaps
Applicable Anal. 89,1 (2010), 2019-124.
In this work the domain Ω ⊂ R³ is an unbounded periodic waveguide (see
Fig.1.b), like a necklace, which consists of an infinite "needle" and an infinite
number of bounded "beads" (translates of a fixed bounded cell). We make the
geometry of the domain to depend on a positive parameter h > 0, which describes
the distance of two adjacent beads. Due to the unboundedness of the domain,
the essential spectrum S of the elasticity problem is not empty. Using general
results one can show that the spectrum S has a band-gap structure:
it is the union of infinitely many (bounded) intervals, or bands,
I(k) ⊂ R⁺. Our aim
becomes
to show that the intervals I(k) do not overlap, implying the existence of spectral gaps.
To this end, on the limit h → 0, the spectral elasticity problem corresponds to the
case where the domain is bounded and Lipschitz, and the spectrum is
discrete. Considering the cases with h > 0 as a perturbation of the limit
case, we are able to control the lower and upper bounds of spectral bands I(k)
and assure that for small enough h, spectral gaps are created in a controlled
way.
- G.Cardone, S.A.Nazarov, J.Taskinen:
Criteria for the existence of the essential spectrum
for beak-shaped elastic bodies.
J.Math. Pur. Appl. 92, 6 (2009), 628-650.
An example of a beak shaped domain Ω in R³
is presented in Fig.4. The boundary
irregularity is angular in two (horizontal) dimensions and cuspidal in one (vertical)
dimension. The geometric parameter γ > 0 describes the cuspidal sharpness;
if it were equal to 0, the beak would be turned into a corner domain.
We consider the spectral problem for the linear elasticity system
in the domain Ω with traction-free boundary conditions, see Formula 1.
The main result of the paper, Theorem 4.2 claims that the essential spectrum
is nonempty, if and only if γ ≥ 1. For 0 < γ < 1 the spectrum is
thus fully discrete.
The main technical device is a new weighted anisotropic Korn-type
inequality.
We end the paper by a discussion of the possibility of cuspidal
structures to act as "black holes" for elastic waves. Our results
give a mathematical explanation to the following phenomenon: hitting
a trapezoidal metal brick with a hammer, the brick does cling, but
a similar brick with cuspidal edges does not (see Fig.5).
-
G.Cardone, S.A.Nazarov, J.Taskinen:
`Absorption'' effect for elastic waves by the beak-shaped
boundary irregularity.
Doklady Physics 54, 3 (2009), 146-150.
This is related to the previous paper.
Back to main page .
|