[Yleistä]
[Regressioanalyysin tulosten
tulkinta]
[Usean muuttujan regressioanalyysi]
[Regressioanalyysin rajoitteet]
[Lähteet]
[Kalvot]
Regressioanalyysi
Regressioanalyysin (regression analysis) avulla
tutkitaan yhden tai useamman selittävän muuttujan vaikutusta selitettävään
muuttujaan. Sen avulla voidaan pyrkiä vastaamaan esimerkiksi siihen vaikuttaako
koulutuksen pituus saadun palkan suuruuteen ja jos vaikuttaa, niin kuinka
voimakas tämä vaikutus on. Regressioanalyysin erityinen etu on, että siinä
voidaan tutkia yhtä aikaa monen selittävän muuttujan vaikutusta selitettävään
muuttujaan. Tällöin tuloksen kertovat, mikä on yksittäisen selittävän muuttujan
osuus silloin kuin muiden vaikuttavien tekijöiden vaikutus selitettävään
muuttujaan on otettu huomioon.
Regressioanalyysi
on monipuolinen ja joustava menetelmä muuttujien välisten kausaalisuhteiden
tutkimukseen. Sen edellytyksenä on, että selitettävä muuttuja on vähintään
välimatka-asteikollinen (katso »muuttujien mittaustaso). Selittävät muuttujat ovat yleensä myös
vähintään välimatka-asteikollisia, mutta myös luokittelu- ja
järjestysasteikollisia muuttujia voidaan sisällyttää analyysiin. Tällöin niistä
täytyy tehdä ns. dummy-muuttujia.
Regressiosuora ja -kerroin
Regressioanalyysin
perusperiaatteet voidaan esittää havainnollisesti kuvion 1 avulla. Hajontakuviossa
on esitetty 15 valtion lukutaidottomuusprosentti ja valtion panostus
koulutukseen prosenttiosuutena bruttokansantuotteesta. Jokainen kuvion piste
viittaa yhteen maahan. Esimerkiksi Intiassa oli vuonna 1999 lukutaidottomia
noin 48% väestöstä ja maan bruttokansantuotteesta käytettiin 3,3%
koulutusmenoihin. Kannattaa huomata, että kuviossa esitetyt maat ja luvut ovat
oikeita, mutta niiden valinta perustui tarkoituksenmukaisuusharkintaan. Näin
esitetyt empiiriset tulokset ovat yleistettävyyden kannalta parhaimmassakin
tapauksessa vain suuntaa-antavia.
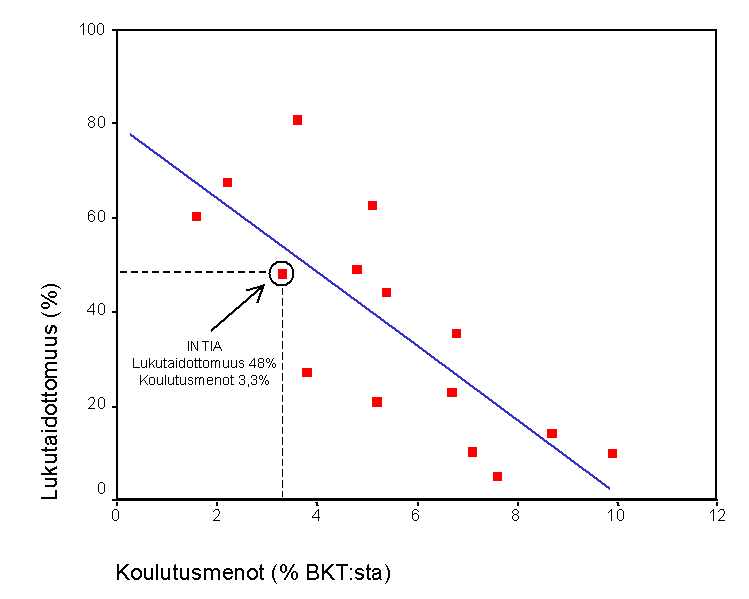
Kuvio 1.
Lukutaidottomuusprosentti (1991) ja koulutusmenot (% BKT:sta, 1995). Lähde:
Tilastokeskus, Maailma numeroina.
Kuviosta näkee
selvästi, miten lukutaidottomuus ja panostus koulutukseen ovat yhteydessä
toisiinsa. Mitä suurempi osuus maan bruttokansatuotteesta sijoitetaan
koulutukseen, sitä vähemmän maassa on lukutaidottomia. Regressioanalyysin
avulla voidaan tutkia, onko näiden kahden muuttujan välinen yhteys
tilastollisesti merkitsevä. Lisäksi regressioanalyysi kertoo, kuinka vahva
yhteys on, eli kuinka paljon lukutaidottomuus vähenee, kun koulutusmenojen
osuus kasvaa.
Kuvioon piirretty
viiva on ns. regressiosuora (regression line). Se osoittaa
muuttujien välisen yhteyden voimakkuuden. Jos regressiosuora laskee alaspäin,
on muuttujilla negatiivinen yhteys ja jos se nousee ylöspäin, on niillä
positiivinen yhteys. Mitä lähempänä vaakatasoa suora on, sitä vähemmän
muuttujilla on yhteyttä toisiinsa.
Regressiosuora
voidaan merkitä kaavan avulla seuraavasti:
Y = a + bX
Kaavassa Y
tarkoittaa selitettävän muuttujan arvoa, a on ns. vakiotekijä, X on selittävän
muuttujan arvo ja b on regressiokerroin (regression coefficient).
Regressiokerroin on regressiosuoran kulmakerroin. Jos se saa negatiivisen
arvon, on suora laskeva ja jos regressiokerroin on positiivinen, on suora
nouseva. Jos regressiokerroin on nolla, ei muuttujien välillä ole lineaarista
eli suoraviivaista yhteyttä. Vakiotekijä kertoo, minkä arvon selitettävä
muuttuja saa silloin, kun selitettävän muuttujan X arvo on nolla. Se siis
kertoo, missä kohtaa regressiosuora leikkaa kuvion y-akselin.
Regressioanalyysin
avulla voidaan selvittää kaavan vakiotekijän ja regressiokertoimen arvot. Esimerkiksi
kuvion 1 aineiston perusteella saadaan seuraava regressioyhtälö:
Y = 80 – 7,9X
Yhtälön
regressiokerroin (eli b:n arvo) on –7,9. Regressiokerroin kertoo, kuinka paljon
selitettävä muuttuja muuttuu, kun selittävä muuttuja kasvaa yhden yksikön. Esitetty
yhtälö voidaan tulkita seuraavasti. Kun koulutusmenoja lisätään yhdellä
prosenttiyksiköllä bruttokansantuotteesta, vähenee lukutaidottomien määrä 7,9
prosenttiyksikköä. Vakiotekijä kertoo, kuinka paljon maassa olisi
lukutaidottomia, jos koulutusmenot olisivat nolla eli maassa ei panostettaisi
laisinkaan rahaa koulutukseen. Tällöin lukutaidottomia olisi maassa 80%. Tämä
on tietenkin vain hypoteettinen arvio, koska maailmasta tuskin löytyy sellaista
maata, missä koulutukseen ei panostettaisi ollenkaan.
Regressiomallin
eli –yhtälön pätevyyttä voidaan arvioida sen mukaan, kuinka lähelle kuvion
pisteet sijoittuvat regressiosuoraa. Mitä lähempänä suoraa ne sijaitsevat, sitä
parempi on regressiomallin selitysvoima ja päinvastoin. Jos kuvion pisteen
sijoittuvat hyvin lähelle suoraa, on mallilla hyvä ennustevoima, koska sen
avulla voidaan hyvin tarkasti arvioida, mikä on jonkin yksittäisen maan
lukutaidottomuusprosentti silloin, kun tiedetään kuinka paljon maassa
sijoitetaan koulutukseen. Mitä kauempana pisteet suorasta sijaitsevat, sitä
epävarmempia ovat ennusteet.
Yksittäisen
havainnon arvon etäisyyttä regressiosuorasta kutsutaan havainnon virhetermiksi
tai residuaaliksi (residual). Esimerkiksi kuviosta 1 tiedämme,
että Intiassa lukutaidottomuuden taso on 48%. Regressioyhtälön avulla voidaan
myös laskea regressiomallin ennusteen Intian lukutaidottomuudelle. Se saadaan
sijoittamalla regressiokaavaan selitettävän muuttujan eli koulutukseen menevien
varojen bruttokansantuoteosuus, joka on Intian kohdalla 3,3. Näin saadaan
regressiomallin ennusteeksi Intian osalta 53,9 (=80-7,9*3,3). Tämä osoittaa,
että regressiomalli ei ole aivan tarkka yksittäisten havaintojen kohdalla.
Intian virhetermi mallissa on 48-53,9=-5,9. Mitä suuremmat mallin virhetermit
itseisarvoltaan ovat, sitä huonompi ennustearvo regressiomallilla on ja
päinvastoin.
Regressioanalyysin tulosten tulkinta
Seuraavaksi
käytetään Tilastokeskuksen keräämää Maailma numeroina –aineistoa
regressioanalyysin tulosten esittelemiseksi (katso »aineiston kuvaus). Selitettävänä
muuttujana on maakohtainen elinajan odote eli väestön keskimääräisen
odotettavissa olevan eliniän pituus. Elinajan odotteeseen vaikuttaa tietenkin
useat eri tekijät, mutta esimerkkiregressioanalyysissa käytetään keskeisenä
selittävänä tekijänä HIV-taudin levinneisyyttä. HI-virus ja siitä seuraava
AIDS-tauti on 1990-luvulla kääntänyt monessa maassa aikaisemmin kasvussa olleet
elinajan odotteet laskuun. Suurimmillaan tämä vaikutus näkyy Afrikassa.
Arvioiden mukaan esimerkiksi Zimbabwessa odotettavissa oleva elinikä on
laskenut AIDSin vaikutuksesta jopa 26 vuotta (U.S. Bureau of Census 1998). AIDS
vaikuttaa elinajan odotteeseen kahdella eri tavalla. Ilman kallista lääkitystä
sairaus tappaa aikuiset potilaat nopeasti. Lisäksi sairaus kasvattaa lapsikuolleisuutta,
koska taudin voi saada myös HI-virusta kantavalta äidiltä. Näiden kahden
tekijän kautta AIDSilla on suuri vaikutus odotettavissa olevaan elinikään.
Aineistossa on
165 maata, joista on saatavilla tiedot sekä elinajan odotteesta että HIV-potilaiden
määrästä. Vuonna 1999 eliniän odote vaihteli 36.3 (Malawi) ja 83.5 (Andorra)
vuoden välillä. HIV-tapausten yleisyyttä mitataan suhteuttamalla ne väestön
kokoon niin, että muuttuja mittaa HIV-tapausten yleisyyttä suhteessa 1000
henkilöön. Tämä muuttuja vaihtelee lähes nollan (esimerkiksi Suomessa 0,21) ja
182 (Botswana) välillä.
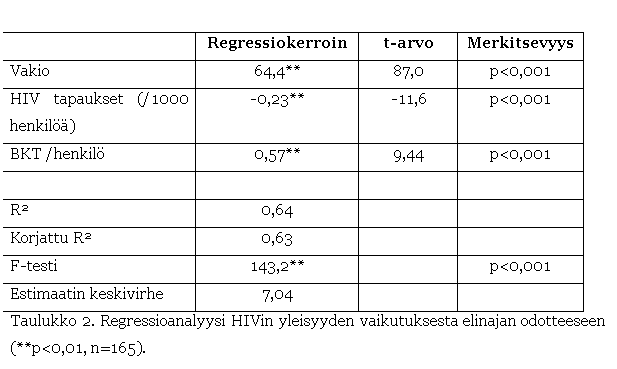
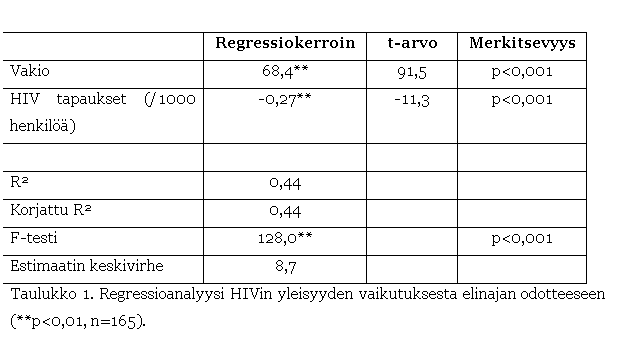
Taulukossa 1 on
esitetty regressioanalyysin tulokset. Taulukon yläosassa ovat analyysin
selittävät muuttujat, niiden regressiokertoimet, t-arvot ja merkitsevyystiedot.
Taulukon alaosa sisältää regressiomallin pätevyyden arviointiin sopivia
tunnuslukuja.
Ennen regressiokertoimien
varsinaista tulkintaa kannattaa kiinnittää huomiota niiden tilastolliseen
merkitsevyyteen. Regressioanalyysin yhteydessä testataan jokaisen selittävän
muuttujan osalta onko niillä vaikutusta selitettävään muuttujaan eli eroavatko
ne tilastollisesti merkitsevästi nollasta (katso »tilastollinen päättely ja »hypoteesien testaus). Tällaiseen
tarkoitukseen sopiva testimenetelmä on ns. t-testi. Testin tuloksena jokaiselle
selittävälle muuttujalle saadaan t-arvo, jonka suuruus ratkaisee sen, voidaanko
muuttujan kerrointa pitää nollaa suurempana tilastollisten kriteerien mukaan.
Taulukon viimeisessä sarakkeessa on esitetty t-testien merkitsevyystasot. Ne
osoittavat, että sekä vakiotermi että HIV-tapausten laajuuden regressiokerroin
eroavat tilastollisesti selvästi nollasta. Kaikki regressioanalyysiin sopivat
ohjelmat tuottavat nämä tunnusluvut automaattisesti.
Taulukon 1
tulokset siis osoittavat, että HIV-tapausten levinneisyys laskee odotettavissa
olevaa elinikää (regressiokertoimen etumerkki on negatiivinen). Kerroin on
arvoltaan –0,27, mikä tarkoittaa sitä, että HIV-tapausten suhteellisen osuuden
kasvu yhdestä hengestä kahteen henkeen tuhannesta laskee elinajan odotetta 0,27
vuotta. Tämä on suuri muutos. Jos Suomessa (0,21 tapausta / 1000 henkilöä) HIV
olisi yhtä yleinen kuin Ranskassa (2,21 / 1000 henkilöä), suomalaisten
keskimääräinen elinajan odote olisi noin
puoli vuotta matalampi ((2,21-0,21)*0,27=0,54). Jos HIV-tapauksia olisi
suhteellisesti yhtä paljon kuin Tansaniassa (39,6 / 1000 henkilöä),
suomalaisten elinajan odote olisi peräti 11 vuotta lyhyempi
((39,6-0,21)*0,27=10,6).
Taulukon 1
alalaidassa on esitetty tärkeimmät regressioanalyysin selitysvoimaa kuvaavat
testit. Tällaisia testejä on useita, mutta R2-luku ja F-testi ovat yleisemmin
käytetyt. R2-luku on regressiomallin selitysosuus. Se kertoo
kuinka suuren osuuden selitettävän muuttujan vaihtelusta regressionanalyysin
selittävät muuttujat pystyvät selittämään. R2-luku vaihtelee nollan
ja yhden välillä. Se saadaan laskemalla selitettävän muuttujan arvojen ja
mallin tuottamien ennustearvojen korrelaation neliö. Jos R2-luku on
pieni regression selittävät muuttujan pystyvät selittämään vain vähän
selitettävän muuttujan vaihtelusta ja päinvastoin. Taulukossa 1 R2-luku
on 0.44. Tämä tarkoittaa, että HIV-tapausten levinneisyydellä pystytään siis
kohtuullisen hyvin selittämään elinajan odotteen vaihtelua. Regressiomallin
avulla 44% elinajan odotteen vaihtelusta voidaan selittää pelkästään
HIV-tapausten suhteellisella määrällä. On kuitenkin huomattava, että
selitysosuutta kuvaavat luvut ovat merkityksellisiä nimenomaan regressiomallin
asettamassa kontekstissa. Jos elinajan odotetta selitettäisiin lisäksi muilla
siihen vaikuttavilla tekijöillä, HIVin levinneisyyden selitysosuus olisi luultavasti
pienempi.
Korjattua R2-lukua (adjusted R2)
käytetään silloin, kun halutaan verrata kahden regressioanalyysin tuloksia
keskenään. Korjattu R2-luku ottaa huomioon mallin sisältämien
selittävien muuttujien lukumäärän. Se on arvoltaan aina pienempi tai yhtä suuri
kuin varsinainen R2-luku. Korjaus R2-lukuun tarvitaan sen
vuoksi, että uusien selittävien muuttujien lisääminen regressioanalyysiin
nostaa aina R2-lukua, vaikka nämä lisätyt muuttujat eivät
todellisuudessa pystyisikään lisäämään selityskykyä. Silloin kun
tarkasteltavana on vain yksi regressiomalli, ei korjatun R2-luvun
käyttäminen ole tarpeellista, mutta regressiomalleja verratessa siitä on
hyötyä. Jatkossa taulukon 1 regressioanalyysia laajennetaan uusilla
muuttujilla. Siksi korjattu R2-luku on raportoitu myös tässä
yhteydessä, jotta vertaileminen myöhemmin esitettyihin laajennettuihin
regressiomalleihin on mahdollista.
F-testi on tilastollinen testi, joka kertoo
pystytäänkö regressioanalyysissa olevilla muuttujilla ylipäänsä selittämään selitettävän
muuttujan vaihtelua. Koska se on tilastollinen testi, saadaan sille myös
merkitsevyystaso. Taulukossa 1 F-testin tulos on erittäin merkitsevä. Tämä ei
sinänsä ole yllätys, koska myös selittävän muuttujan regressiokerroin on
tilastollisesti merkitsevä. On kuitenkin mahdollista, että yhdenkään selittävän
muuttujan regressiokerroin ei ole tilastollisesti merkitsevä, mutta F-testin
tulos on. Tämä tarkoittaa sitä, että regressioanalyysin muuttuja pystyvät
yhdessä selittämään selitettävän muuttujan vaihtelua, vaikka yksittäin katsoen
ne eivät ole tilastollisesti merkitseviä. Tällaiset tapaukset ovat kuitenkin
harvinaisia.
Viimeinen
regressiomallin onnistuneisuutta kuvaava tunnusluku on estimaatin keskivirhe
(standard error of estimate). Tämä luku ilmoittaa regressiomallin
virhetermien keskihajonnan (katso »hajontaluvut). Mitä suurempi se on, sitä suurempi on
virhetermien hajonta ja samalla sitä pienempi mallin selitysvoima. Estimaatin
keskivirheen suuruus riippuu aina regressiomallin hyvyyden lisäksi selitettävän
muuttujan mittaluokasta. Taulukossa 1 se on 8,7, mikä on kohtalaisen suuri
luku, kun se suhteutetaan elinajan odotteen vaihteluväliin (36-84 vuotta). Tämä
osoittaa, että HIV-tapausten yleisyydestä tietyssä maassa ei pystytä kovinkaan
tarkasti ennustamaan maan väestön odotettavissa olevaa keskimääräistä elinikää.
Usean muuttujan regressioanalyysi
Edellisissä
regressioanalyysin esimerkeissä oli vain yksi selittävä muuttuja.
Regressioanalyysin etu on kuitenkin se, että siihen voi sisällyttää useita
selittäviä muuttujia yhtäaikaisesti. Tällöin muuttujien regressiokertoimet
kertovat, kuinka paljon selitettävän muuttujan arvo muuttuu, kun selittävän
muuttujan arvo muuttuu yhdellä yksiköllä ja kaikkien muiden muuttujien arvo
pysyy samana. Toisin sanoen usean muuttujan regressioanalyysissa
regressiokertoimet ilmoittavat selittävän muuttujan vaikutuksen selitettävään
muuttujaan niin, että muiden mallin muuttujien vaikutus on vakioitu.
Kahden selittävän
muuttujan regressioanalyysin kaava voidaan esittää seuraavasti:
Y = a + b1X1 + b2X2
Kaavassa Y on
selitettävän muuttujan arvo, a vakiotekijä, X1 ja X2
selittävät muuttujat sekä b1 ja b2 niiden
regressiokertoimet.
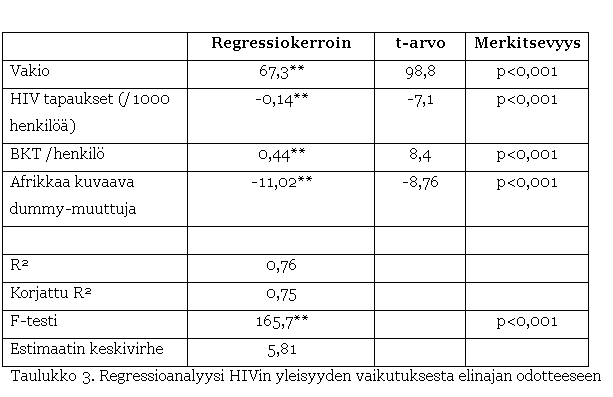
Taulukon 2
korjattu R2-luku luku osoittaa, että BKT-muuttujan lisääminen
regressiomalliin paransi mallin selityskykyä huomattavasti verrattuna Taulukon
1 tuloksiin. Taulukossa 1 korjattu R2-luku on 0,44 ja taulukossa 2
vastaava tunnusluku on 0,63. Lisäksi estimaatin keskivirhe pieneni 8,7:stä
7,0:an. Nämä molemmat tunnusluvut kertovat, että käyttämällä BKT-muuttujaan
HIV-muuttujan ohella analyysissa, pystytään eri maiden odotettavissa olevaa
elinikää ennustamaan paremmin kuin tyytymällä ainoastaan HIV-muuttujan
käyttöön.
Dummy-muuttujat
Y = a + b1X2 + b2X2
+ b3X3
Dummy-muuttujia voidaan
käyttää myös tilanteessa, jossa laatu- tai järjestysasteikon muuttuja saa
useampia kuin kaksi vaihtoehtoa. Tällaisessa tilanteessa yleinen periaate on,
että uusia dummy-muuttujia täytyy luoda yksi vähemmän kuin laatu- tai
järjestysasteikon muuttujassa on vastausvaihtoehtoja. Jos esimerkiksi
laatueroasteikon muuttuja voi saada neljä eri arvoa, täytyy regressioanalyysia
varten luoda kolme uutta dummy-muuttujaa.
Oletetaan, että
tutkija haluaa regressioanalyysin avulla selvittää henkilöiden iän ja koulutuksen
vaikutusta heidän palkkatasoonsa. Koulutus on mitattu kolmiasteisella
mittarilla, jonka vaihtoehdot ovat peruskoulu, keskiasteen tutkinto ja
korkeakoulututkinto. Regressioanalyysin tarpeisiin tästä muuttujasta täytyy
luoda kaksi uutta dummy-muuttujaa. Ensimmäinen muuttuja voisi olla
peruskoulu-dummy, joka saa arvon yksi jos vastaaja on suorittanut vain
peruskoulun. Muutoin muuttuja saa arvon nolla. Toinen muuttuja olisi
keskiaste-dummy, joka saa arvon yksi silloin kun vastaajalla on keskiasteen tutkinto
ja arvon nolla muutoin. Tutkija laskee regressioanalyysin, jossa selitettävänä
muuttujana on vastaajan palkan suuruus markkoina ja selittävinä muuttujina
vastaajan ikä sekä kaksi edellä mainittua dummy-muuttujaa.
Useamman
dummy-muuttujan tapauksessa niiden regressiokertoimien tulkinta tulee hiukan
hankalammaksi, koska ne täytyy tulkita toisiinsa suhteuttaen. Oletetaan, että
regressioanalyysin tuloksissa peruskoulu-dummyn regressiokerroin on –5000 ja
keskiaste-dummyn –2000. Nämä kertoimet tulee tulkita suhteessa
korkeakoulututkinnon suorittaneiden palkkaan. Ne kertovat, että ainoastaan
peruskoulun suorittaneiden palkka on keskimäärin 5000 mk pienempi kuin
korkeakoulun suorittaneiden palkat. Keskiasteen tutkinnon suorittaneiden
keskimääräinen palkka on 2000 mk pienempi kuin korkeakoulututkinnon
suorittaneiden. Dummy-muuttujien regressiokertoimet ilmoittavat siis ryhmän
keskimääräisen poikkeaman siitä ryhmästä, jolle ei tehty omaa dummy-muuttujaa.
Päätökset siitä,
mille vastausvaihtoehdoille omat dummy-muuttujat luodaan ja mikä vaihtoehto
jätetään analyysista pois eivät ole kovin ratkaisevia. Ne toki vaikuttavat
dummy-muuttujien regressiokertoimien arvoihin, mutta niistä tehtävät tulkinnat
ovat kuitenkin samoja. Jos edelliseen regressiomalliin olisikin lisätty
keskiaste- ja korkeakoulu-dummyt, olisivat niiden regressiokertoimet olleet
+3000 ja +5000 mk. Ne siis kertovat, että korkeakoulun käyneiden ja peruskoulun
käyneiden keskimääräinen ero palkoissa on 5000 mk sekä korkeakoulun käyneiden
ja keskiasteenkoulutuksen saaneiden 2000 mk.
Regressioanalyysin rajoitteet
Lähteet
Lisätietoja
Yhteiskuntatieteellisten
tutkimusalojen opiskelijat ja tutkijat voivat perehtyä suomeksi
regressioanalyysin perusteisiin muun muassa seuraavissa kirjoissa:
- Alkula, Tapani & Pöntinen, Seppo
& Ylöstalo, Pekka (1994): Sosiaalitutkimuksen kvantitatiiviset
menetelmät. WSOY, Juva.
- Karma, Kai & Komulainen, Erkki
(1992): Käyttäytymistieteiden tilastomenetelmien jatkokurssi.
Yliopistopaino, Helsinki.
- Nummenmaa, Tapio & Konttinen,
Raimo & Kuusinen, Jorma & Leskinen, Esko (1996): Tutkimusaineiston
analyysi. WSOY, Porvoo.
- Toivonen, Timo (1999): Empiirinen
sosiaalitutkimus: filosofia ja metodologia. WSOY, Porvoo.
Englanniksi
regressioanalyysin perusteista voi lukea mm. seuraavista kirjoista. Näistä De
Vausin kirja sisältää vain regressioanalyysin perusteet, mutta toisaalta se on
vasta-alkajalle erittäin helppolukuinen. Tabachnickin ja Fidellin kirjassa on
huomattavasti kattavampi regressioanalyysin esittely.
- De Vaus, D.A. (1994): Surveys in Social Research. Third edition. UCL Press, Guildford.
- Tabachnick, Barbara G. & Fidell, Linda S. (1996): Using Multivariate Statistics. Harper Collins, New York.
Sagen
julkaisemassa määrällisten menetelmien opassarjassa on useita selkeitä
regressioanalyysikirjoja. Näistä Lewis-Beckin kirja on helppolukuisin.
- Berry, William D. (1993): Understanding Regression Assumptions. Sage, Newbury Park.
- Berry, William D. & Feldman, Stanley (1985): Multiple Regression in Practice. Sage, Beverly Hills.
- Fox, John (1991): Regression Diagnostics. Sage, Newbury Park.
- Hardy, Melissa A. (1993): Regression with Dummy Variables. Sage, Newbury Park.
- Lewis-Beck, Michael S. (1980): Applied Regression: An Introduction. Sage, Beverly Hills.
- Ostrom, Charles W. jr (1990): Time Series Analysis. Sage, Beverly Hills.
- Sayrs, Lois W. (1989): Pooled Time Series Analysis. Sage, Newbury Park.
Tilastotieteelliseltä kannalta regressioanalyysia
käsitellään seuraavissa teoksissa:
·
Bohrnstedt, George W. & Knoke, David (1988): Statistics for
Social Data Analysis. Toinen painos. F.E. Peacock Publishers, Itasca.
·
Moore, David S. (1995): The Basic Practice of Statistics. W.H.
Freeman and Company, New York.
·
Moore, David S. & McCabe, George P. (1999): Introduction to the
Practice of Statistics. W.H. Freeman and Company, New York.
Kaikkein
kattavimmin regressioanalyysista kerrotaan kansantaloustieteen ekonometrian
oppikirjoissa. Kirjat voivat pikaisen silmäyksen perusteella vaikuttaa
vaikeilta. Niihin kannattaa silti tutustua, jos haluaa oppia syvällisesti
erilaisista regressioanalyysin käyttömahdollisuuksista. Verrattain
helppolukuisia, mutta siitä huolimatta kattavia ekonometrian oppikirjoja ovat
mm.:
- Gujarati, Damodar N. (1988): Basic Econometrics. McGraw-Hill, New York.
- Kennedy, Peter (1998): A Guide to Econometrics. MIT Press, Boston.
- Kmenta, Jan (1986): Elements of Econometrics. MacMillan, New York.
- Pindyck,
Robert S. & Rubinfeld, Daniel L. (1997): Econometric Models and
Economic Forecasts. Irwin,
Boston.
Verkosta löytyy runsaasti
regressioanalyysiin liittyvää materiaalia. Katso esimerkiksi David Garsonin ”Statnotes: an Online Textbook” –sivujen regressioanalyysia käsittelevä
osuus osoitteessa:
Myös ”Statistics Resource
Centre” –sivustolla käsitellään lyhyesti regressioanalyysia osoitteessa:
- http://www.millsaps.edu/www/socio/regression.htm
Seuraavasta
osoitteesta löytyy pieni java-applet, jonka avulla voi interaktiivisesti
testata regressioanalyysin perusperiaatteita:
TV:stä tutut
animaatiohahmot Ren ja Stimpy opettavat hauskasti regressioanalyysin perusteita
osoitteessa:
Kalvot
- Regressioanalyysin avulla tutkitaan
yhden tai useamman selittävän muuttujan vaikutusta selitettävään
muuttujaan
- Esim. vaikuttaako koulutuksen pituus
palkan suuruuteen?
- Voidaan tutkia yhtä aikaa monen
muuttujan vaikutusta selitettävään muuttujaan
- Selittävän muuttujan oltava vähintään
välimatka-asteikollinen
- Selittävät muuttujat vähintään
välimatka-asteikollisia tai ns. dummy-muuttujia
- Esim. lukutaidottomuus ja
koulutusmenot
- Kuvio 1.
- Regressiosuora osoittaa muuttujien
välisen riippuvuuden voimakkuuden.
- Regressiosuora: Y = a + bX
- Y on selitettävä muuttuja, X on
selittävä muuttuja
- A on vakiotekijä
- b on regressiokerroin
- Regressiokerroin kertoo kuinka paljon
Y muuttuu, kun X muuttuu yhden yksikön
- Jos b<0, yhteys negatiivinen (X:n
kasvaessa Y pienenee)
- Jos b>0, yhteys positiivinen (X:n kasvaessa Y suurenee)
- Jos b=0, ei lineaarista eli
suoraviivaista yhteyttä muuttujien välillä
- Regressiomallin ennustekyky riippuu
siitä, kuinka lähellä havainnot ovat regressiosuoraa
- Jos ne ovat lähellä -> hyvä
ennustekyky
- Jos ne ovat kaukana -> huono
ennustekyky
- Virhetermi (residuaali) on havainnon
arvon erotus regressiosuorasta (eli mallin ennustearvosta)
- Esimerkki: selittääkö HIVin
esiintyvyys odotettavissa olevaa elinikää?
- Taulukko 1.
- Kun HIVin määrä kasvaa väestössä
yhdellä hengellä tuhatta henkeä kohden, lyhenee väestön keskimääräinen
eliniän odote 0,27 vuotta
- Mallin hyvyyden arviointi:
- R2 –luku kertoo
selitysosuuden
o
kuinka suuri
osuus Y:n vaihtelusta voidaan selittää X:n vaihtelulla?
- F-testi kertoo pystyvätkö X-muuttujat
ylipäänsä selittämään Y:n vaihtelua?
- SEE kertoo virhetermien keskihajonnan
- Usean muuttujan regressioanalyysi
- Kaavana: Y = a + b1X1
+ b2X2
- Regressiokertoimet ilmaisevat kuinka
paljon Y muuttuu kun X muuttuu yhden yksikön ja kaikki muut selittävät
muuttujat pysyvät vakiona
- Esimerkki 2: HIV+BKT selittää
elinikää
- Taulukko 2.
- Dummy-muuttujat
- Luokittelu- tai järjestysasteikon
muuttuja voidaan sisällyttää analyysiin tekemällä niistä dummy-muuttujia
- Dummy-muuttuja saa vain kaksi arvoa:
0 tai 1
- Regressiokerroin ilmaisee, kuinka
paljon tutkittu ryhmä (dummy=1) eroaa muista (dummy=0)
- Jos luokittelumuuttujassa n
vaihtoehtoa, täytyy luoda n-1 dummy-muuttujaa
- Esimerkki 3. HIV+BKT+Afrikkaa koskeva
dummy selittävät elinikää
- Taulukko 3.
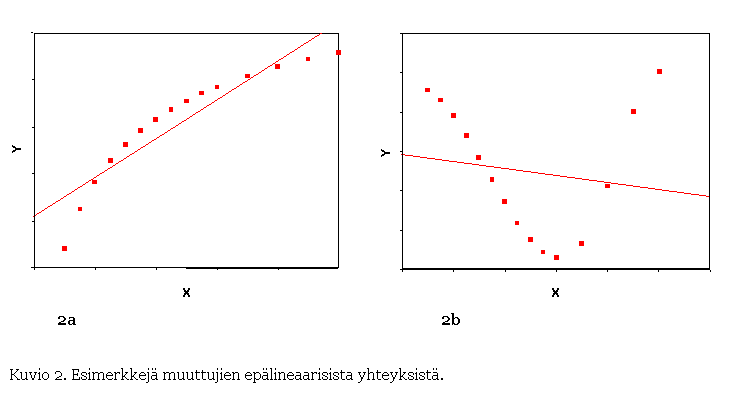
- Regressioanalyysin rajoitteet:
- Lineaarisuusoletus
- Voidaan usein korjata muuttujan
muunnoksilla
- Kuvio 2.
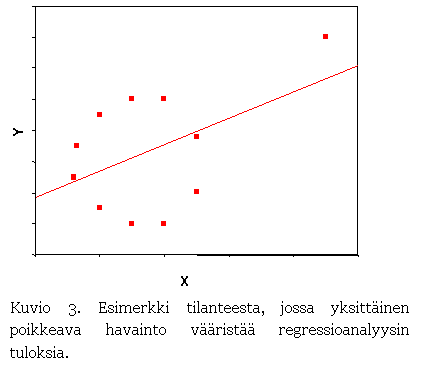
- Poikkeavat havainnot eli outlieri-tapaukset
- Voivat vääristää tuloksia
- Kuvio 3.
- Multikollineaarisuus: selittävät
muuttujat korreloivat liian voimakkaasti keskenään
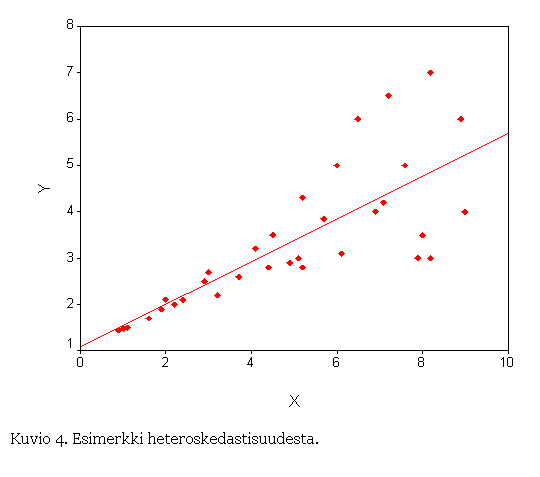
- Heteroskedastisuus: virhetermien hajonta
riippuvainen X:n arvoista
- Kuvio 4.
- Havaintojen aikariippuvuus
- Ongelma aikasarja-analyysissa
- Havaintojen virhetermit korreloivat
keskenään
- Esim. tämän vuoden työttömyys on
osittain riippuvainen viime vuoden työttömyydestä