LOGISTINEN REGRESSIO

[Esimerkki logistisesta regressioanalyysista]

Logistinen regressio

Logistinen regressioanalyysi on tavanomaisen »regressioanalyysin erityistyyppi. Sitä käytetään silloin, kun selitettävä muuttuja voi saada vain kaksi arvoa. Voidaan esimerkiksi pyrkiä selittämään sitä, miten eri tekijät vaikuttavat siihen, onko vastaaja naimisissa vai ei.

Tavallisessa regressioanalyysissa selitettävän muuttujan arvot voivat vaihdella paljonkin. Regressioanalyysi ei kuitenkaan ole käyttökelpoinen silloin, kun selitettävän muuttujan arvot rajoittuvat vain kahteen vaihtoehtoon. Logistinen regressioanalyysi ei pyri ennustamaan määriä, vaan todennäköisyyksiä. Kyse on siis siitä, millä todennäköisyydellä tarkasteltavana oleva asia tapahtuu tai pätee. Tulokset kertovat, vaikuttavatko selittävät muuttujat tapahtuman todennäköisyyteen ja kuinka suuri vaikutus on. Esimerkiksi äänestämistutkimuksen tulokset voivat kertoa, että naisilla on suurempi todennäköisyys äänestää kuin miehillä tai että iän kasvaessa osallistumistodennäköisyys kasvaa.

Logistisen regressiomallin idea

Logistisessa regressioanalyysissa selitettävä muuttuja täytyy koodata niin, että se voi saada ainoastaan arvon yksi tai nolla. Oletetaan, että tutkimuksessa on tarkoitus selvittää, mitkä tekijät vaikuttavat ihmisten äänestysaktiivisuuteen. Selitettävä muuttuja mittaa sitä, äänestikö vastaaja viime vaaleissa. Se saa arvon nolla, jos vastaaja ei äänestänyt (eli Y=0) ja arvon yksi jos hän äänesti (Y=1).

Logistisen regressioanalyysin ymmärtämiseksi täytyy tietää, mitä riskisuhteella tarkoitetaan. Oletetaan, että äänestystutkimuksen otoksessa naisista 70 % ja miehistä 60 % ilmoitti äänestäneensä viime vaaleissa. Näiden lukujen avulla voidaan naisille ja miehille laskea ns. riskisuhde (odds ratio). Riskisuhdetta käytetään yleisesti esimerkiksi kuvattaessa vedonlyönnin voittosuhteita. Riskisuhde saadaan suhteuttamalla naisten äänestämistodennäköisyys miesten vastaavaa lukuun. Näin saadaan tulokseksi 1,17 (=0,7/0,6), mikä tarkoittaa sitä, että naisilla on 1,17 kertaa suurempi todennäköisyys äänestää kuin miehillä. Riskisuhde voidaan laskea myös toisinpäin. Miesten todennäköisyys äänestää on 0,86-kertainen (=0,6/0,7) naisten vastaavaan todennäköisyyteen verrattuna.

Riskisuhde voi saada arvoja nollan ja äärettömän välillä. Tavanomainen regressioanalyysi soveltuu kuitenkin parhaiten tilanteeseen, missä selitettävän muuttujan arvoja ei ole rajattu millekään ennalta määrätylle välille. Siksi logistista regressioanalyysia varten riskisuhteesta otetaan vielä logaritmi. Tämä varmistaa sen, että saatu luku vaihtelee äärettömän pienien ja äärettömän suurien lukujen välillä.

Yksinkertaistettuna logistinen regressiomalli on tavallinen regressiomalli, jossa selitettävänä muuttujana on riskisuhteen logaritmi. Tämä voidaan ilmaista kaavalla seuraavasti:

Kaavassa P(Y=1) on todennäköisyys sille, että selitettävä muuttuja saa arvon yksi, a on vakiotekijä, b regressiokerroin ja x selittävän muuttujan arvo. Logistisen regressiomallin kaavan lauseke a+bx on täsmälleen sama kuin normaalissa regressioanalyysissä. Siksi logistisen regressiomallin tulkinta ja siihen liittyvät ongelmat ovat lähes samat kuin regressioanalyysissa.

Tulkinnassa täytyy kuitenkin ottaa huomioon se, että logistisessa regressiomallissa selittävien ja selitettävän muuttujan suhde ei ole lineaarinen, vaan siinä oletetaan suhteen seuraavan niin sanotun s-käyrän (eli logistisen käyrän) muotoa. Kuviossa 1 on esitetty kuvitteellinen esimerkki logistisista käyristä. Esimerkissä selittävä muuttuja x-akselilla saa arvoja nollasta kymmeneen. Logistisen regressioanalyysin tulos on y-akselilla. Logistisessa regressioanalyysissa selitettävän tapahtuman todennäköisyys saa arvoja nollan ja yhden välillä.

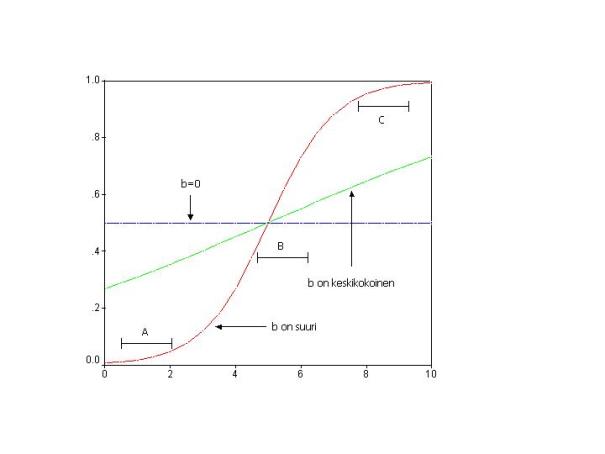
Kuvio 1. Esimerkkejä logistisesta s-käyrästä.

Jos selittävällä ja selitettävällä muuttujalla ei ole lainkaan yhteyttä toisiinsa logistisessa regressiomallissa, saa regressiokerroin b itseisarvoltaan hyvin pienen arvon. Kuten kuviosta 1 nähdään, on muuttujien yhteyttä kuvaava käyrä täysin vaakasuora silloin, kun b saa arvon nolla. Tämä osoittaa sen, että selitettävän muuttujan mittaaman tapahtuman todennäköisyys ei muutu ollenkaan selittävän muuttujan arvojen vaihdellessa. Silloin kun kerroin b saa suuren arvon, on selittävän muuttujan arvojen ja tapahtuman todennäköisyyden yhteyttä kuvaava käyrä s-kirjaimen muotoinen. Tämä tarkoittaa sitä, että jos selittävän muuttujan pieni arvo kasvaa hiukan, ei tämä muuta paljoakaan selitettävän muuttujan mittaaman tapahtuman todennäköisyyttä (väli A). Sen sijaan selittävän muuttujan saadessa arvoja vaihteluvälin keskivaiheilta pienikin muutos aiheuttaa suuren muutoksen selitettävän ilmiön tapahtumistodennäköisyydessä (väli B). Selittävän muuttujan ollessa lähellä ylärajaa muutoksilla on jälleen pienempi vaikutus (väli C).

Kun kertoimen b arvo on keskikokoinen, on sen muoto vaakasuoran ja s-käyrän välimailla. Jos kertoimen arvo on negatiivinen, laskee selitettävän muuttujan mittaaman tapahtuman todennäköisyys selittävän muuttujan arvon kasvaessa. Tällöin logistiset käyrät ovat samanmuotoisia kuin kuviossa 1, mutta ne laskevat vasemmalta oikealle.

Logistisen regressiomallin kertoimien tulkinta eroaa tavallisen regressiomallin kertoimien tulkinnasta siinä, että tavallisessa regressiomallissa yhden yksikön muutos selittävässä muuttujassa aiheuttaa aina samansuuruisen muutoksien selitettävässä muuttujassa. Sen sijaan logistisessa regressioanalyysissa selitettävän todennäköisyyden muutos riippuu b-kertoimen lisäksi selittävän muuttujan arvosta. Tämän takia logistisen regressiomallin tulosten tulkinta on aina hankalampaa kuin tavallisessa regressiomallissa.

Esimerkki logistisesta regressioanalyysista

Logistisen regressioanalyysin esimerkissä tutkitaan, mitkä tekijät vaikuttavat suomalaisten protektionismin kannatukseen. Vuoden 1996 World Values Surveyn Suomen osa-aineistossa (katso »aineistokuvaus) on kysymys, jossa vastaajien piti valita kahdesta vaihtoehdosta, kumpi on heidän mielestään parempi (v133). Nämä vaihtoehdot olivat 1) ”Muissa maissa valmistettuja tuotteita voidaan tuoda tänne ja myydä täällä, jos ihmiset haluavat ostaa niitä” ja 2) ”Ulkomaisten tuotteiden myynnille Suomessa pitäisi olla enemmän esteitä, jotta voitaisiin suojella tämän maan ihmisten työpaikkoja”. Näistä jälkimmäinen edustaa protektionistista ajattelutapaa.

Vastaajista noin 40 prosenttia valitsi ensimmäisen ja noin 60 prosenttia jälkimmäisen vaihtoehdon. Analyysia varten muuttuja on koodattu niin, että ensimmäinen vaihtoehto saa arvon nolla ja jälkimmäinen arvon yksi. Näin logistisen regressioanalyysin avulla voidaan tutkia siis, mitkä tekijät vaikuttavat vastaajien todennäköisyyteen valita protektionistinen vaihtoehto.

Analyysin selittäjinä käytetään viittä eri muuttujaa. Demografisista muuttujista mukana ovat vastaajan ikä (v216) ja sukupuoli (v214, koodattu dummy-muuttujaksi seuraavasti: mies=0, nainen=1). Vastaajan tulotasoa mitataan 10-luokkaisella muuttujalla (v227), jossa suuret arvot tarkoittavat korkeampia tuloja. Asennemuuttujista mukana on vastaajien ylpeys suomalaisuudestaan (v205). Se on mitattu neliportaisella asteikolla, jossa pienet arvot kuvaavat suurempaa ylpeyttä. Hypoteesina on, että ne vastaajat, jotka ovat ylpeitä suomalaisuudestaan ovat valmiimpia kannattamaan protektionismia. Lisäksi analyysissa on mukana muuttuja, joka kuvaa vastaajan sijoittumista politiikan vasemmisto-oikeisto -ulottuvuudella (v123). Se saa arvoja yhdestä kymmeneen pienten arvojen kuvastaessa sijoittumista vasemmalle. Oletuksena on, että vasemmalle identifioituvat vastaajat todennäköisemmin hyväksyvät protektionistiset ajatukset ulottuvuuden oikeaan laitaan sijoittuvat vastaajat.

Muuttuja	Regressiokerroin	Merkitsevyys
Vakio	-0.00	p=0,99
Sukupuoli (nainen=1, mies=0)	0,48**	p=0,001
Ikä	0,02**	p<0,001
Ylpeys suomalaisuudesta (1=suuri … 4=heikko)	-0,10	p=0,33
Sijoittuminen vasemmisto-oikeisto -ulottuvuudella (1-10)	-0,07	p=0,11
Tuloluokka (1-10)	-0,08*	p=0,01

Taulukko 1. Logistinen regressioanalyysi protektionismin kannatukseen vaikuttavista tekijöistä.

Logistisen regressioanalyysin tulokset ovat taulukossa 1. Mallin toimivuuden tarkastelu kannattaa aloittaa muuttujien merkitsevyystasojen analyysilla. Vastaajien poliittista sijoittumista ja heidän ylpeyttään suomalaisuudesta kuvaavat muuttujat eivät ole tilastollisesti merkitseviä tekijöitä protektionismin selittäjinä. Sen sijaan muut muuttujat ovat tilastollisesti merkitseviä. Ikä-muuttujan regressiokerroin on positiivinen, mikä kertoo sen, että vanhemmat ihmiset ovat valinneet protektionistisen vaihtoehdon nuorempia todennäköisemmin. Myös sukupuolimuuttuja on positiivinen eli naiset valitsevat miehiä todennäköisemmin protektionistisen vaihtoehdon. Tuloluokkamuuttuja saa negatiivisen kertoimen. Se kertoo, että suurituloisilla on pienituloisempia vähäisempi todennäköisyys kannattaa protektionistista vaihtoehtoa.

Logistisen regressiomallin ennustearvoa voidaan tarkastella katsomalla, kuinka hyvin sen avulla pystytään luokittelemaan vastaajat oikeisiin luokkiin heidän vastaustensa mukaan. Taulukon 1 regressiomalli ennustaa oikein 80 prosenttia niistä vastaajista, jotka valitsivat protektionistisen vaihtoehdon. Toisaalta malli ennustaa oikein vain 37 prosenttia niistä, jotka valitsivat vapaata kauppaa arvostavan vaihtoehdon. Näin mallin ennustekyky on parhaimmillaankin vain kohtalainen. Toisin sanoen taulukon 1 sisältämien muuttujien avulla ei pystytä ennustamaan kovinkaan tarkasti vastaajien kantaa protektionismiin. Samalla on huomattava, että selitettävänä muuttujana ollut protektionismimittari on hyvin karkea, ja suhtautumista olisikin kannattanut mitata laajemmalla skaalalla. Logistista regressioanalyysia onkin tarkoituksenmukaisinta käyttää silloin, kun selitettävää ilmiötä ei ole mitattu tai ei voida mitata tarkemmin kuin kaksijakoisesti.

Multinomiaalinen logistinen regressio

Multinomiaalinen logistinen regressio (multinomial logistic regression) on tavallisen logistisen regressioanalyysin laajennus, jossa selitettävä muuttuja voi saada useampia kuin pelkästään kaksi vaihtoehtoa. Kuvitellaan esimerkiksi tilanne, jossa luokitteluasteikolla mitattu selitettävä muuttuja voi saada kolme eri vaihtoehtoa: A, B ja C. Multinomiaalisessa logistisessa regressioanalyysissa tutkitaan, mitkä tekijät vaikuttavat siihen, että vastaaja on valinnut tietyn vaihtoehdon suhteessa muihin vaihtoehtoihin. Käytännössä tämä tarkoittaa sitä, että tässä esimerkkitapauksessa tuloksena saadaan kolme erilaista mallia. Yhdessä verrataan vaihtoehdon A valintaa suhteessa vaihtoehtoon B, toisessa A:n valintaa suhteessa C:hen ja kolmannessa B:n valintaa suhteessa C:hen.

Tässä yhteydessä ei käsitellä multinomiaalista logistista regressioanalyysia tarkemmin. Menetelmästä kiinnostuneen kannattaa katsoa ’Lisätietoja’ –osuudesta kirjallisuusvinkkejä.

Lisätietoja

Suomen kielellä logistisesta regressioanalyysista ei toistaiseksi löydy kattavaa yleisesittelyä. Englanniksi menetelmää on käsitelty mm .Tabachnickin ja Fidellin kirjassa:

· Tabachnick, Barbara G. & Fidell, Linda S. (1996): Using Multivariate Statistics. Harper Collins, New York.

Sagen määrällisten menetelmien opassarjassa on useita logistista regressioanalyysia käsitteleviä kirjoja. Alla mainituista teoksista Liaon kirjassa käsitellään myös multinomiaalista logistista regressiota.

· Liao, Tim Futing (1994): Interpreting Probability Models. Logit, Probit, and Other Generalized Linear Models. Sage, Thousand Oaks.

· Menard, Scott (1995): Applied Logistic Regression Analysis. Sage, Thousand Oaks.

· Pampel, Fred C. (2000): Logistic Regression. A Primer. Sage, Thousand Oaks.

Verkossa David Garsonin ”Statnotes: an Online Textbook” on hyvä lähde logistiseen regressiomalliin ja sen tulosten tulkintaan liittyvissä asioissa. Suora osoite on:

· http://www2.chass.ncsu.edu/garson/pa765/logistic.htm

Kalvot

o Logistinen regressioanalyysi on normaalin regressioanalyysin erityistyppi

o Käytetään tilanteissa, jossa selitettävä muuttuja voi saada vain kaksi arvoa

o Esimerkiksi:

o Äänestikö vastaaja viime vaaleissa?

o Onko vastaaja naimisissa?

o Logistisen regression avulla tutkitaan jonkun tapahtuman tai asiantilan todennäköisyyteen vaikuttavia tekijöitä

o Vaikuttavatko selittävät muuttujat tilastollisesti merkitsevästi tapahtuman todennäköisyyteen?

o Kuinka suuri tämä vaikutus on?

o Logistisessa regressioanalyysissa selitettävän ja selitettävien muuttujien suhde ei ole lineaarinen vaan se seuraa ns. s-käyrän muotoa

o Kuvio 1

o Esimerkki logistisesta regressioanalyysista

o Mitkä tekijät vaikuttavat vastaajien protektionismin kannatukseen?

o Taulukko 1

o Multinomiaalinen logistinen regressio

o Normaalin logistisen regressioanalyysin laajennus

o Selitettävä muuttuja voi saada kolme tai useampi vaihtoja

o Esimerkiksi vastaaja äänesti joko hallituspuolueen ehdokasta, oppositiopuolueen ehdokasta tai ei äänestänyt laisinkaan