Ristiintaulukon riippumattomuustesti

Kuten aiemmin todettiin täytyy otokseen perustuvat ristiintaulukot alistaa ns. riippumattomuustestille, joka kertoo kuinka todennäköistä on, että riippuvuus on syntynyt ainoastaan otantasattuman vaikutuksesta niin, että muuttujat ovat perusjoukossa toisistaan riippumattomia. Yleisimmin käytetty testi on ns. Pearsonin χ²-testi, joka perustuu havaittujen ja odotettujen frekvenssien vertailuun.

Taulukko 1 on jo aiemmin käytetty esimerkkiristiintaulukko sukupuolen ja poliittisista asioista keskustelemisen aktiivisuuden suhteesta. Taulukkoon on kuitenkin lisätty muutamia lukuja, joita tarvitaan χ²-testin laskemiseksi. Normaalisti näitä tietoja ei tietenkään tarvitse raportoida, koska kaikki tilasto-ohjelmistot laskevat testin automaattisesti tai ainakin pyydettäessä. Taulukkoon on ensinnäkin lisätty ”yhteensä” sarake sen oikeaan laitaan. Näitä lukuja tarvitaan odotettujen frekvenssien laskemiseen. Luvut osoittavat, että 72 vastaajaa ilmoitti keskustelevansa usein politiikasta ystäviensä kanssa, 621 silloin tällöin jne.

Taulukko 1. Aktiivisuus keskustella poliittisista asioita ystävien kanssa sukupuolen mukaan (havaitut frekvenssit, odotetut frekvenssit ja prosenttijakauma).

	Mies	Nainen	Yhteensä
Usein	43 35,0 9 %	29 37,0 6 %	72
Silloin tällöin	323 301,9 68 %	298 319,1 60 %	621
En koskaan	108 137,1 23 %	174 144,9 35 %	282
Yhteensä n	100 % 474	100 % 501	975

Jokaiseen ristiintaulukon soluun on myös lisätty prosenttiluvun yläpuolelle kaksi lukua. Ensimmäinen näistä on havaittu solufrekvenssi (observed frequency). Esimerkiksi 43 naista ja 29 miestä vastasi keskustelevansa usein ystäviensä kanssa politiikasta. Tämän luvun alla on solun odotettu frekvenssi (expected frequency), eli luku, joka osoittaa kuinka monta vastaajaa solussa todennäköisesti olisi, jos miehet ja naiset eivät eroaisi toisistaan keskustelutapojensa suhteen. Jos keskusteluaktiivisuus todellakin olisi täysin riippumaton sukupuolesta olisi todennäköisintä, että silloin 35,0 miestä ja 37,0 naista vastaisivat keskustelevansa politiikasta usein. Syy sille, että naisten odotettu frekvenssi on hiukan miesten vastaavaa suurempi, johtuu siitä, että otoksessa on hiukan enemmän naisia kuin miehiä.

Odotetut frekvenssit voidaan laskea seuraavasta kaavasta:

jossa

= i:nnen rivin ja j:nnen sarakkeen odotettu (Expected) frekvenssi

= i:nnen rivin reunajakauma (eli rivin valinneiden vastaajien kokonaissumma)

= j:nnen sarakkeen reunajakauma (eli sarakkeen valinneiden vastaajien kokonaissumma)

N = Havaintojen määrä taulukossa

Esimerkiksi ”En koskaan” vastaavien miesten odotettu frekvenssi saadaan laskemalla (282*474)/975=137,1. Vastaava luku naisten osalta on 144,9 (=(282*501)/975).

Kuten jo aiemmin todettiin, χ²-testi perustuu havaittujen ja odotettujen frekvenssien eroille. Käytännössä testissä lasketaan ns. χ²-luku, joka kuvastaa sitä, kuinka paljon havaitut ja odotetut frekvenssit eroavat toisistaan. Kun χ²-luku on suuri, eroavat nämä frekvenssit paljon toisistaan ja kun se on pieni, ovat erot havaittujen ja odotettujen frekvenssien välillä pienet. χ²-luku laskentaan seuraavan kaavan avulla:

jossa

= i:nnen rivin ja j:nnen sarakkeen odotettu frekvenssi

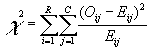
= i:nnen rivin ja j:nnen sarakkeen havaittu frekvenssi

R = Rivien määrä

C= Sarakkeiden määrä.

Käytännössä em. kaava tarkoittaa sitä, että jokainen ristiintaulukon solu käydään läpi ja jokaisessa niissä lasketaan ensin odotetun ja havaitun frekvenssin erotus, joka sen jälkeen korotetaan neliöön. Tämän jälkeen saatu tulos jaetaan odotetun frekvenssin arvolla. Lopuksi nämä solukohtaiset arvot lasketaan kaikki yhteen ja lopputuloksena on koko ristiintaulukon χ²-luku.

Esimerkiksi yllä olevan taulukon χ²-luku saadaan kaavasta

(43-35,0)²/35,0+(29-37,0)²/37,0+(323-301,9)²/301,9+(298-319,1)²/319,1+(108-137,1)²/137,1+(174-144,9)²/144,9=18,4

Lopuksi tarvittava p:n arvo saadaan χ²-jakaumasta, joka löytyy taulukkona esimerkiksi useimpien metodioppaiden liitteenä. Käytännössä tietenkin tilasto-ohjelmistot antavat tarvittavan p-arvon suoraan. Oikean p-arvon saamiseen tarvitaan vielä vapausasteiden määrä. Ristiintaulukossa vapausasteiden määrä saadaan kaavasta (rivien määrä-1)*(sarakkeiden määrä-1). Koska esimerkkitaulukossa rivejä on kolme ja sarakkeita on kaksi, on vapausasteiden määrä 2*1 eli 2. Näiden tietojen avulla oikea p-arvo voidaan hakea taulukoista. Tässä tapauksessa se on selvästi pienempi kuin 0,01 eli χ²-testin tulos on tilastollisesti erittäin merkitsevä ja näin ollen nollahypoteesi (eli olettamus siitä, että otoksessa havaittu miesten ja naisten ero johtuu pelkästään sattumasta) voidaan hylätä. Miehet todellakin keskustelevat ystäviensä kanssa politiikasta enemmän kuin naiset.