[»Yleistä]

[»Variaatiosuhde]

[»Vaihteluväli]

[»Vaihteluvälin pituus]

[»Keskihajonta]

[»Variaatiokerroin]

[»Lisätietoja]

[»Kalvot]

Hajontaluvut

»Keskilukujen lisäksi hajontaluvut ovat erittäin yleisiä muuttujan jakaumaa kuvaavia mittalukuja. Hajontaluvut kertovat, kuinka muuttujan arvot vaihtelevat käytetyn keskiluvun ”ympärillä”. Kahdella muuttujalla voi olla sama keskiluku (esimerkiksi keskiarvo), mutta niiden hajonta voi olla täysin erilainen. Siksi muuttujan jakaumaa kuvatessa on tapana esittää sekä sopiva keskiluku että hajontaluku.

Samoin kuin keskiluvuissa muuttujan »mittaustaso vaikuttaa soveltuvan hajontaluvun valintaan. Taulukossa 1 on esitetty, mitkä hajontaluvut sopivat millekin muuttujan mittaustasolle.

Taulukko 1. Sopivan hajontaluvun valinta muuttujan mittaustason mukaan (X = voi käyttää, - = ei voi käyttää).

		Muuttujan mittaustaso
		Luokitteluasteikko	Järjestysasteikko	Välimatka-asteikko	Suhdeasteikko
	Variaatiosuhde	X	X	X	X
Hajontaluku	Vaihteluväli	-	X	X	X
	Vaihteluvälin pituus	-	-	X	X
	Keskihajonta	-	-	X	X
	Variaatiokerroin	-	-	X	X

Taulukossa 2 on esitetty kuvitteellinen aineisto, jota käytetään erilaisten hajontalukujen esittelemiseksi. Siinä on kolme eri mittaustason muuttujaa.

Taulukko 2. Kuvitteellinen aineisto työpaikan kymmenestä työntekijästä.

Työntekijän havaintonumero	Sukupuoli	Koulutus	Lapsien määrä
Työntekijä 1	Mies	Peruskoulu	0
Työntekijä 2	Nainen	Keskiaste	4
Työntekijä 3	Nainen	Keskiaste	1
Työntekijä 4	Mies	Korkeakoulu	1
Työntekijä 5	Nainen	Keskiaste	2
Työntekijä 6	Nainen	Korkeakoulu	1
Työntekijä 7	Nainen	Korkeakoulu	1
Työntekijä 8	Mies	Peruskoulu	0
Työntekijä 9	Mies	Korkeakoulu	0
Työntekijä 10	Nainen	Keskiaste	2

Variaatiosuhde

Variaatiosuhde (variation ratio) on hajontaluku, jota voidaan käyttää luokitteluasteikollisen muuttujan yhteydessä. Se on helppo laskea ja ymmärtää. Variaatiosuhde kertoo, kuinka suuri osuus havainnoista on muuttujan »moodiluokassa. Variaatiosuhde (v) lasketaan kaavasta:

v=1-(havaintojen määrä moodiluokassa / havaintojen määrä)

Variaatiosuhde vaihtelee nollan ja yhden välillä. Se saa arvon nolla, jos kaikki muuttujan arvot ovat moodiluokassa. Tässä tapauksessa muuttujan arvot eivät tietenkään vaihtele ollenkaan, joten on luontevaa, että hajontaluku saa arvon nolla. Mitä lähempänä yhtä variaatiosuhde on, sitä enemmän aineistossa on hajontaa.

Taulukon 2 aineistossa lapsiluvun yleisin arvon on yksi (eli se on muuttujan moodiluokka) ja aineistossa on neljä työntekijää, joilla on yksi lapsi perheessään. Näin aineiston variaatiosuhde on 1-(4/10)=0,6.

Sukupuolimuuttujan yleisin arvo on ’nainen’, joita on aineistossa kuusi. Näin variaatiosuhde on tämän muuttujan osalta 1-(6/10)=0,4.

Koulutusmuuttujan osalta aineistossa on kaksi moodia (’keskiaste’ ja ’korkeakoulu’). Variaatiosuhde lasketaan siitä muuttujan luokasta, jossa on eniten havaintoja. Koska tässä tapauksessa on kaksi tällaista luokkaa, ei ole väliä kummasta variaatiosuhde lasketaan. Se on koulutuksen osalta 1-(4/10)=0,6.

Variaatiosuhdetta käytetään yleensä vain luokitteluasteikollisten muuttujien yhteydessä. Muuttujan ollessa välimatka- tai suhdeasteikollinen sen käyttö ei useimmiten ole järkevää, vaan on luonnollista valita jokin hajontaluku, joka sopii paremmin tähän tarkoitukseen. Välimatka- tai suhdeasteikon muuttuja voi saada suuren määrän erilaisia arvoja jollain tietyllä välillä. Tällaisessa tapauksessa variaatiosuhteen käyttäminen hajontalukuna ei ole mielekästä, koska on epätodennäköistä, että moodiluokassa olisi kovinkaan monta havaintoa. Jos tutkitaan esimerkiksi nettopalkkoja jollain tietyllä teollisuuden alalla, on epätodennäköistä, että löytyisi suuri ryhmä työntekijöitä, joilla on täsmälleen sama palkka.

Vaihteluväli

Vaihteluväli (range) on järjestys-, välimatka- ja suhdeasteikon muuttujille sopiva hajontaluku. Se ilmoittaa yksinkertaisesti pienimmän ja suurimman muuttujan arvon välin. Määritelmän mukaan vaihteluväli on W=[x₁, x_n] silloin kun havaintojen arvon on sijoitettu suuruusjärjestykseen aloittaen pienimmästä muuttujan arvosta. x₁ viittaa edellisessä kaavassa aineiston pienimpään arvoon ja x_n sen suurimpaan arvoon.

Esimerkiksi taulukon 2 aineistossa lapsien lukumäärän pienin arvo on nolla ja suurin arvo neljä. Näin vaihteluväli on W=[0,4]. Koulutuksen osalta vaihteluväli on W=[”peruskoulu”, ”korkeakoulu”]. Koska sukupuolimuuttuja on luokitteluasteikollinen, siitä ei ole järkevää tarkastella vaihteluväliä.

Vaihteluvälin pituus

Kun muuttuja on mitattu välimatka- tai suhdeasteikolla, voidaan puhua vaihteluvälin pituudesta. Se on yksinkertaisesti muuttujan suurimman ja pienimmän arvon erotus. Kaavana se voidaan ilmaista seuraavasti:

w=x_n-x₁

Kaavassa w on vaihteluvälin pituus, x_n muuttujan suurin arvo ja x₁ muuttujan pienin arvo.

Esimerkiksi taulukon 2 aineistossa lapsilukumuuttujan vaihteluvälin pituus on 4-0=4.

Keskihajonta

Keskihajonta (standard deviation) on hajontaluku välimatka- tai suhdeasteikon muuttujille. Keskihajonta on ehkä kaikkein yleisimmin käytetty hajontaluku. Keskihajonta kuvaa sitä, kuinka kaukana yksittäiset muuttujan arvot ovat keskimäärin muuttujan »aritmeettisesta keskiarvosta. Keskihajonta (s) lasketaan kaavasta

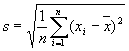
Kaavassa x_i viittaa i:nnen havainnon arvoon ja tarkoittaa aineiston aritmeettista keskiarvoa. Sigma -merkki (Σ) tarkoittaa yhteenlaskua. Esitetyssä kaavassa lasketaan jokaisen havainnon arvon erotus koko aineiston keskiarvosta. Tämän jälkeen erotus korotetaan neliöön. Tämän jälkeen kaikki saadut arvot lasketaan yhteen. Tämä saatu summa jaetaan havaintojen määrällä (n) ja saadusta tuloksesta otetaan vielä neliöjuuri keskihajonnan saamiseksi. Mitä suurempi saatu arvo on, sitä enemmän muuttujan arvoissa on hajontaa ja päinvastoin.

Edellä mainittu keskihajonnan kaava on tarkoitettu tilanteisiin, jossa on tarkasteltavana koko »perusjoukko. Jos kyse on »otoksesta käytetään usein termiä otoskeskihajonta ja silloin täytyy käyttää hieman erilaista kaavaa. Tällöin kaava on

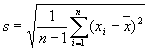
Tässä kaavassa jakajana on havaintojen määrä vähennettynä yhdellä. Etenkin suurissa aineistoissa ero näiden kahden kaavan antamilla keskihajontaluvuilla on pieni.

Jos oletetaan, että taulukon 2 aineisto on koko perusjoukko (eli kaikki työpaikan työntekijät) saadaan lapsiluvun keskihajonnaksi (ensimmäisen kaavan mukaan) 1,17. Jos taas oletetaan, että kyseessä on iso työpaikka ja aineisto on vain kymmenen hengen otos koko perusjoukosta, saadaan keskihajonnaksi (jälkimmäisen kaavan mukaan) 1,23. Ero on pieni, vaikka aineisto koostuikin vain kymmenestä havainnosta.

Keskihajonnan käsitteeseen liittyy usein myös varianssin käsite. Varianssilla tarkoitetaan keskihajonnan neliötä (s²). Varianssia käytetään monessa »tilastolliseen päättelyyn liittyvässä yhteydessä.

Variaatiokerroin

Kahden eri otoksen keskihajontojen keskinäinen vertailu on joskus ongelmallista, koska keskihajonta vaihtelee aineiston keskiarvon myötä. Variaatiokerroin (coefficient of variation) on hajontaluku, joka suhteuttaa keskihajonnan aineiston keskiarvoon. Se lasketaan kaavasta

V=s/

Kaavassa s on muuttujan keskihajonta ja on muuttujan keskiarvo. Käytännössä siis keskihajonta suhteutetaan muuttujan keskiarvoon. Näin kahden ryhmän hajonnan vertailu on mielekkäämpää.

Lisätietoja

Keskeisimmät hajontaluvut on esitelty kaikissa tilastotieteiden ja kvantitatiivisten menetelmien perusoppaissa. Hyvä suomenkielinen opastus on esimerkiksi:

• Heikkilä, Juha (1993): Tilastotieteen ABC-kirja 1. Yliopistopaino, Jyväskylä.

Englannin kielellä hajontaluvuista ja niiden sovelluksista yhteiskuntatieteellisessä tutkimuksessa voi lukea esimerkiksi seuraavista teoksista:

• Jones, Laurence F. & Olson, Edward C. (1996): Political Science Research. A Handbook of Scope and Method. Addison Wesley Longman, New York.
• De Vaus, D.A. (1994): Surveys in Social Research. Third edition. UCL Press, Guildford.

Verkosta lisätietoa keskiluvuista löytyy mm. Hyperstat Online palvelusta. Siellä kerrotaan mm. sellaisista jakauman tunnusluvuista, joita ei tässä yhteydessä käsitelty. Hyperstat Onlinen osoite on:

• http://davidmlane.com/hyperstat/index.html

Ja hajontaluvuista kerrotaan erityisesti sivulla:

• http://davidmlane.com/hyperstat/desc_univ.html

Toinen hyvä verkkoresurssi on Gene V. Glassiin pitämän ”Intro to Quant Methods” –kurssin sivut osoitteessa:

• http://glass.ed.asu.edu/stats/

Jakauman tunnuslukuja käsitellään erityisesti sivulla:

• http://glass.ed.asu.edu/stats/lesson2/

Kalvot

• Hajontaluvut kuvaavat muuttujan arvojen vaihtelun suuruutta
• Sopivan hajontaluvun valinta riippuu muuttujan mittaustasosta
• Taulukko1

o Variaatiosuhde

• Käytetään lähinnä luokitteluasteikollisten muuttujien yhteydessä
• Kertoo, kuinka suuri osuus havainnoista sijoittuu muuttujan moodiluokkaan
• Kaava: v=1-(havaintojen määrä moodiluokassa/havaintojen määrä)
• Vaihtelee nollan (ei hajontaa) ja yhden välillä (suuri hajonta)

• Vaihteluväli
• Sopii järjestys-, välimatka- ja suhdeasteikon muuttujille
• Ilmoittaa pienimmän ja suurimman arvon välin
• W=[x₁,x_n]

• Vaihteluvälin pituus

o Sopii välimatka- ja suhdeasteikon muuttujille

• Ilmoittaa suurimman ja pienimmän arvon erotuksen
• w=x_n-x₁

• Keskihajonta
• Sopii välimatka- ja suhdeasteikon muuttujille
• Kuvaa, kuinka kaukana yksittäiset havaintojen arvot ovat koko aineiston keskiarvosta
• Keskihajonnan kaava
• Varianssi on keskihajonnan neliö

• Variaatiokerroin
• Käytetään haluttaessa verrata kahden ryhmän keskihajontoja
• Suhteuttaa keskihajonnan keskiarvoon
• v = keskihajonta / keskiarvo