FAKTORIANALYYSI

Faktorianalyysi

Tutkiessaan potilasta lääkäri kysyy häneltä erilaisista taudin oireista: särkeekö päätä tai vatsaa, onko kuumetta tai väsymystä jne. Nämä oirekuvaukset johtavat diagnoosiin eli päätelmään siitä, mikä sairaus potilasta vaivaa. Lääkäri ei siis suoraan pysty tunnistamaan tautia, vaan hän tekee sen epäsuorasti taudin aiheuttamien oireiden perusteella. Tällainen päättelytapa kuvaa hyvin faktorianalyysia. Faktorianalyysissa pyritään löytämään havaintoyksikön ominaisuuksia kuvaavasta muuttujajoukosta piileviä yhdenmukaisuuksia eli faktoreita. Ajatuksena on, että tiettyjä havaintoyksikköjen ominaisuuksia ei pystytä havainnoimaan suoraan, vaan niistä saadaan ainoastaan epäsuoraa tietoa. Faktori voidaan käsittää eräänlaisena hypoteettisena konstruktiona tai teoreettisena käsitteenä, jonka olemassaolo päätellään konkreettisista havainnoista. Yhteiskuntatieteiden alalla tällaisia käsitteitä ovat esimerkiksi ’konservatiivisuus’, ’sosiaalisuus’, ’älykkyys’ tai ’työpaikan ilmapiiri’.

Tyyppiesimerkki faktorianalyysista on älykkyyden mittaaminen. Älykkyyttä ei voida suoraan havainnoida, mutta erilaisten älykkyystestien tuloksena ihmisen älykkyydestä on tehty päätelmiä. Lähtökohtana on ollut oletus siitä, että ihmisillä on tietty latentti eli piilevä ominaisuus (älykkyys), josta seuraa havaittavia ilmiöitä (oikeat vastaukset älykkyystestin eri osioihin). Yhteiskuntatieteissä faktorianalyysia käytetään usein mielipidekysymysten analysoinnissa. Jos tutkija haluaa esimerkiksi tutkia ihmisten konservatiivisuutta, ei tätä ominaisuutta voida tarkasti mitata ainoastaan yhden kysymyksen perusteella, vaan ilmiötä monipuolisesti mittaavia kysymyksiä tarvitaan useita. Jotkin näistä kysymyksistä liittyvät suoremmin konservatiivisuuden käsitteeseen, jotkin vähemmän suorasti. Faktorianalyysin avulla voidaan tutkia, muodostavatko annetut vastaukset yhteisen faktorin, joka sitten voidaan tulkita konservatiivisuusfaktoriksi. Tuloksena voi myös olla useita faktoreita, jotka kuvastavat konservatiivisuuden eri ulottuvuuksia.

Faktorianalyysin perusidea

Faktorianalyysissa voidaan erottaa kaksi toisistaan poikkeavaa lähestymistapaa. Eksploratiivinen faktorianalyysi pyrkii etsimään muuttujajoukosta faktoreita, jotka pystyvät selittämään havaittujen muuttujien vaihtelua ilman, että tutkijalla on etukäteen vahvoja odotuksia löydettävien faktoreiden määrästä tai niiden tulkinnasta. Eksploratiivinen faktorianalyysi on siis aineistolähtöinen tutkimusmenetelmä. Analyysin tuloksena voidaan löytää yksi tai useampia faktoreita, joita käytetään hyväksi tulosten tulkinnassa. Konfirmatorisessa faktorianalyysissa tutkijalla on jo etukäteen teorian pohjalta muodostettu käsitys aineiston faktorirakenteesta ja analyysin tehtävänä on joko varmistaa tai kumota tämä käsitys empiirisen aineiston pohjalta. Eksploratiivinen faktorianalyysi on näistä kahdesta faktorianalyysin muodosta yleisempi, joten tässä yhteydessä esittely keskittyy lähinnä siihen. Lopussa käsitellään lyhyesti myös konfirmatorista faktorianalyysia.

Kuviossa 1 on esitetty faktorianalyysin perusidea yksinkertaistetun kaavion muodossa. Kuviossa on kaksi faktoria ja seitsemän havaittua muuttujaa. Muuttujat voivat olla esimerkiksi kyselylomakkeen seitsemän väittämää, joilla on pyritty mittaamaan vastaajien konservatiivisuutta. Faktorit ovat tavallaan ’piilomuuttujia’, koska niitä ei voida suoraan havainnoida, vaan niiden olemassaolo päätellään ainoastaan havaittujen muuttujien avulla. Käytännössä faktorin muodostaa joukko muuttujia, jotka korreloivat vahvasti keskenään, mutta vähän muiden muuttujien kanssa. Kuviossa faktoreista lähtee nuolia havaittuihin muuttujiin. Ne kuvaavat faktorianalyysin pohjana olevaa oletusta, jonka mukaan piilevät faktorit aiheuttavat havaitut ilmiöt, eikä päinvastoin.

Faktorianalyysi tuottaa jokaista kuvion nuolen ’vahvuutta’ kuvaavan arvon eli faktorilatauksen (factor loading). Latauksen suuruus kertoo kuinka paljon faktorin avulla pystytään selittämään havaitun muuttujan vaihtelusta. Lataukset saavat arvoja –1 ja 1 välillä. Mitä lähempänä latauksen itseisarvo on yhtä (1) sitä vahvemmin muuttuja latautuu faktorilla (eli sitä paremmin faktori selittää muuttujan vaihtelua). Jos muuttujan lataus on arvoltaan negatiivinen, kertoo se ainoastaan sen, että muuttujan arvot korreloivat negatiivisesti faktorin arvojen kanssa. Jos faktori kuvaa esimerkiksi konservatiivisuutta ja yksi muuttuja saa vahvan, mutta negatiivisen latauksen, tarkoittaa tämä sitä, että konservatiivisia piirteitä omaavat vastaajat ovat vastanneet kysymykseen pienillä arvoilla, kun taas muihin kysymyksiin he ovat vastanneet suurilla arvoilla.

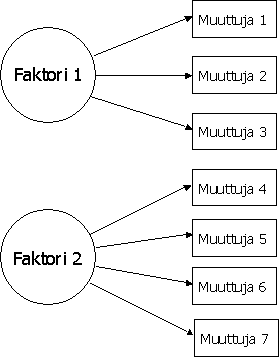
Kuvio 1. Faktorianalyysin idea yksinkertaistettuna.

Faktorimallin toimivuutta voidaan arvioida faktoreiden ominaisarvojen ja havaittujen muuttujien kommunaliteettien avulla. Ominaisarvot (eigenvalue) ilmoittavat, kuinka hyvin faktorit pystyvät selittämään havaittujen muuttujien hajontaa. Mitä suurempi faktorin ominaisarvo on, sitä paremmin se selittää muuttujien hajontaa ja päinvastoin. Kun faktorin ominaisarvo jaetaan havaittujen muuttujien määrällä, saadaan faktorin suhteellinen selitysosuus, joka saa arvoja nollan ja yhden välillä. Selitysosuus kertoo, kuinka suuri osuus kaikkien mallissa mukana olevien havaittujen muuttujien hajonnasta voidaan faktorin avulla selittää. Mitä suurempi osuus on, sitä parempi on faktorin selitysvoima. Kun kaikkien faktoreiden selitysosuudet lasketaan yhteen, saadaan koko analyysin selitysosuus. Se kertoo siis, kuinka suuri osuus kaikkien havaittujen muuttujien hajonnasta voidaan selittää kaikilla löydetyillä faktoreilla.

Kommunaliteetti (communality) puolestaan kertoo, kuinka suuri osuus yksittäisen havaitun muuttujan vaihtelusta selittyy löydettyjen faktorien avulla. Jos muuttujan kommunaliteetti on lähellä yhtä, pystyvät faktorit selittämään sen vaihtelun lähes kokonaan. Toisaalta mitä pienempiä arvo kommunaliteetti saa, sitä huonommin faktorit muuttujaa selittävät. Jos yksittäisen muuttujan kommunaliteetti on pieni, kannattaa harkita, onko muuttujaa ylipäänsä syytä sisällyttää analyysiin.

Esimerkki faktorianalyysista

Faktorianalyysin periaatteet ovat helpoimmin ymmärrettävissä esimerkin avulla. Seuraavassa tehdään faktorianalyysi vuoden 1996 World Values –kyselyn Suomen osa-aineistosta (katso »aineistonkuvaus). Aineiston yksi osuus koostuu 11 asiasta, joiden hyväksyttävyyttä vastaajat arvioivat yksittäin. Kysymys kuului: ”Voisitteko sanoa jokaisesta seuraavaksi luettelemastani asiasta, ovatko ne aina hyväksyttäviä, ei koskaan hyväksyttäviä vai jotain siltä väliltä?”. Vastaajat ilmaisivat hyväksymisensä asteen valitsemalla vastauksensa väliltä 1-10 niin, että arvo 1 tarkoitti ”ei koskaan hyväksyttävä” ja arvo 10 ”aina hyväksyttävä”. Taulukossa 1 on esitetty kaikki 11 arvioitavaa asiaa, niitä vastaavan muuttujan nimi sekä lyhenne, jota käytetään jatkossa muuttujien ilmaisemiseksi.

Muuttuja	Lyhenne	Koko kysymys
v192	sosiaaliturva	Vaatia sairauskorvaus tai sosiaaliturvaetu, johon ei ole oikeutta
v193	kulkuneuvo	Jättää maksamatta julkisessa kulkuneuvossa
v194	verovilppi	Tehdä verovilppiä, jos tilaisuus sallii
v195	varastettu tavara	Ostaa tavaraa, jonka tietää olevan varastettua
v196	lahjukset	Lahjusten ottaminen virkatehtävien hoidossa
v197	homoseksuaalisuus	Homoseksuaalisuus
v198	prostituutio	Prostituutio
v199	abortti	Abortti
v200	avioero	Avioero
v201	eutanasia	Eutanasia, parantumattomasti sairaiden elämän lopettaminen
v202	itsemurha	Itsemurha

Taulukko 1. Faktorianalyysin muuttujat.

Taulukon 1 kaikkiin muuttujiin liittyy moraalisia näkökohtia. Kysymyksen sanamuodossa ei puhuta sanatarkasti siitä, hyväksyvätkö vastaajat asiat omalla kohdallaan. Yleinen sanamuoto on silti kategorinen, koska vastausvaihtoehtojen ääripäät kuvaavat täydellistä hyväksymistä tai kieltämistä. Faktorianalyysi paljastaa muodostavatko kaikki 11 muuttujaa yhteisen faktorin, vai onko tuloksena useita faktoreita. Jos tuloksena on useita faktoreita, on mielenkiintoista nähdä, voidaanko näille faktoreille antaa mielekäs tulkinta. Kuvaavatko ne jäsentyneesti suhtautumisen eri ulottuvuuksia? Aina faktorianalyysin tuloksena ei löydy järkevästi tulkittavaa faktorirakennetta.

Eksploratiivisessa faktorianalyysissa tehtäessä tutkijan tulee aluksi päättää analysoitavien faktorien määrä. Tällaisessa induktiivisesti etenevässä analyysissa faktorien määrää ei ole etukäteen rajattu, joten valinta täytyy tehdä jonkin muun kriteerin perusteella. Yleensä tilasto-ohjelmistot laskevat faktorianalyysin aluksi aineistosta yhtä monta faktoria kuin analyysiin on valittu muuttujia. Kaikkien näin syntyvien ulottuvuuksien käyttö jatkoanalyysissa ei ole kuitenkaan järkevää, koska faktorianalyysin perusideana on tiivistää muuttujien sisältämä informaatio suppeahkoon määrään faktoreita. Edellä mainittiin, että faktorin ominaisarvo kuvaa sitä, kuinka hyvin se pystyy selittämään havaittujen muuttujien hajontaa. Yleisesti käytetty nyrkkisääntö faktorien määrän valinnalle on, että jatkoanalyysiin otetaan vain sellaiset faktorit, joiden ominaisarvo on suurempi kuin yksi. On kuitenkin hyvä muistaa, että tämä sääntö perustuu vain käytäntöön, eikä sille ole mitään vahvaa tilastotieteellistä perustetta. Tilasto-ohjelmistot sisältävät yleensä useita vaihtoehtoisia tapoja faktoreiden lukumäärän määrittelemiseksi.

Seuraava vaihe faktorianalyysissa on niin sanottu faktoreiden rotaatio (rotation). Rotaatiolla (eli faktoriakselien kiertämisellä) viitataan prosessiin, jonka tarkoituksena on tehdä faktorianalyysin tulosten tulkinta helpommaksi Rotaatio ei juurikaan muuta tuloksia sisällöllisesti, se tekee niistä vain helpommin tulkittavia. Rotaatiomenetelmät voidaan jakaa kahteen pääluokkaan. Suorakulmarotaatiomenetelmät (orthogonal rotation) tuottavat sellaisia faktoreita, jotka eivät korreloi keskenään ja vinokulmarotaatiomenetelmät (oblique rotation) puolestaan faktoreita, jotka voivat korreloida keskenään. Tässä yhteydessä ei käsitellä näiden menetelmien yksityiskohtia. ”Lisätietoja” –osuudessa on esitelty kirjoja, joissa kerrotaan tarkemmin rotaation yksityiskohdista (esimerkiksi Nummenmaa ym. 1996). Yleisesti rotaation käyttämistä faktorianalyysin yhteydessä voidaan suositella, koska se lähes poikkeuksetta tekee faktorilatausten teoreettisen tulkinnan helpommaksi.

Palataan taulukon 1 esimerkkiin. Aineisto tuotti kaksi faktoria, joiden ominaisarvo oli suurempi kuin yksi. Taulukkoon 2 on kirjattu esimerkkifaktorianalyysin lopulliset tulokset suorakulmaisen rotaation jälkeen. Rotaatiomenetelmänä käytettiin ns. varimax-rotaatiota.

Analyysi tuotti kahden faktorin mallin, jossa viisi ensimmäistä muuttujaa latautuu vahvimmin toisella faktorilla ja loput muuttujista ensimmäisellä faktorilla. Taulukossa on tummennettu kaikki faktorilataukset, joiden arvo on vähintään 0,5. Entä kuinka suuri latauksen täytyy olla ollakseen merkittävä? Tähän ei ole yksikäsitteistä vastausta. Jotkut oppikirjat suosittelevat alarajaksi arvoa 0,3, toiset taas esimerkiksi 0,5.

Muuttuja	Faktori 1 ’Vapaamielisyys’	Faktori 2 ’Lainkuuliaisuus’	Kommunaliteetti
sosiaaliturva	0,02	0,52	0,27
kulkuneuvo	0,24	0,69	0,53
verovilppi	0,18	0,68	0,50
varastettu tavara	0,14	0,75	0,58
lahjukset	0,03	0,55	0,30
homoseksuaalisuus	0,64	0,03	0,41
prostituutio	0,63	0,23	0,45
abortti	0,80	0,09	0,65
avioero	0,75	0,02	0,56
eutanasia	0,61	0,14	0,39
itsemurha	0,50	0,13	0,27

Ominaisarvo	2,75	2,17
Selitysosuus	25,0%	19,8%

Taulukko 2. Faktorianalyysin tulokset (rotaation jälkeen).

Faktorianalyysista ei ole paljoakaan hyötyä, jos sen tuottamille faktoreille ei pystytä antamaan mielekästä sisällöllistä tulkintaa. Tämän vuoksi tulkinta onkin keskeinen osa faktorianalyysia. Taulukon 2 tulokset viittaavat siihen, että eri asioiden hyväksynnässä voidaan erottaa kaksi ulottuvuutta. Ensimmäisellä faktorilla latautuvat vahvasti sellaiset muuttujat, jotka kuvaavat vastaajien suhtautumista yhteiskunnallisiin ja uskonnollisväritteisiin arvokysymyksiin. Abortti, itsemurha, homoseksuaalisuus jne. ovat perinteisiä ja vuosien saatossa paljon keskustelua herättäneitä yhteiskunnallisia ilmiöitä. Nämä kaikki asiat (eutanasiaa lukuun ottamatta) ovat nyky-Suomessa laillisia, mutta silti jotkut niistä ovat yhä kiistanalaisia. Ensimmäistä faktoria kutsutaan ’vapaamielisyydeksi’.

Toisella faktorilla latautuvat asiat ovat kaikki laittomia tekoja, vaikka useimmat niistä ovat ainakin rikoslain mukaan vain suhteellisen pieniä rikkomuksia (ehkä lahjusten vastaanottoa lukuun ottamatta). Arkielämässä monet ihmiset eivät pidä tällaisia pikkuvilppejä kovinkaan vakavina rikkomuksina. Toinen faktori siis kuvastaa suhtautumista pikkulaittomuuksia kohtaan. Yksinkertaisinta lienee kutsua sitä ’lainkuuliaisuus’-faktoriksi.

Faktorianalyysin tulosten tulkinnassa tulee muistaa, että faktorilatauksista ei voida tulkita mitään siitä, kuinka suuri osa vastaajista hyväksyy tai paheksuu kysymyksissä esitettyjä asioita. Jos tämä on mielenkiinnon kohteena, kannattaa analysoida esimerkiksi muuttujien keskiarvoja ja hajontoja. Faktorianalyysin tulokset kertovat ainoastaan sen, että vastaajat omassa mielessään jaottelevat kysymyksissä luetellut asiat kahden löydetyn ulottuvuuden (faktorin) mukaan.

Tuloksia voidaan tarkastella tarkemmin myös tekniseltä kannalta. Ensimmäisen faktorin ominaisarvo on 2,75 ja sen selitysosuus 25%. Tämä tarkoittaa, että faktori pystyy selittämään neljänneksen kaikkien havaittujen muuttujien hajonnasta, mitä voidaan pitää kohtuullisen hyvänä tuloksena. Faktorin ominaisarvo saadaan ottamalla kaikista faktorilatauksista neliö ja laskemalla saadut arvot yhteen (0,02²+0,24²+…+0,61²+0,50²=2,75). Selitysosuus puolestaan saadaan jakamalla ominaisarvo muuttujien määrällä (2,75/11=0,25). Toisen faktorin selitysosuus on noin 20%, joten kaiken kaikkiaan molemmat faktorit selittävä yhteensä 45% havaittujen muuttujien hajonnasta. Tätä voidaan pitää suhteellisen tyydyttävänä tuloksena.

Muuttujien kommunaliteetit kertovat sen, kuinka hyvin faktorit selittävät yksittäisen muuttujan hajontaa. Kommunaliteetti lasketaan korottamalla muuttujan faktorilataukset neliöön ja laskemalla ne yhteen. Esimerkiksi sosiaaliturvamuuttujan kommunaliteetti saadaan laskemalla 0,02²+0,52²=0,27. Taulukon 2 kaikki kommunaliteetit ovat arvoltaan 0,27 tai suurempia. Tämä tarkoittaa sitä, että analyysista ei tarvinne pudottaa mitään muuttujaa pois. Mitään täsmällistä tilastollista kriteeriä kommunaliteetin arvon riittävälle tasolle ei ole. Muuttujien poistamisessa analyysista täytyy aina käyttää tapauskohtaista harkintaa.

Faktoripisteet

Edellä esitellyt faktorianalyysin tulosten tulkinnat voivat olla sinänsä riittäviä yksittäisen tutkimuksen tarpeisiin. Joskus on kuitenkin mielenkiintoista tietää, miten eri vastaajaryhmät sijoittuvat faktoreiden suhteen. Tällaisessa analyysissa voidaan käyttää hyväksi faktoripisteitä (factor scores), jotka kuvaavat jokaisen aineiston havainnon sijoittumista eri faktoreilla. Faktoripisteet saadaan laskemalla painotettu keskiarvo alkuperäisten muuttujien standardoiduista arvoista. Painoina käytetään faktorilatauksia. Tällä menetelmällä saatujen uusien faktoripistemuuttujien keskiarvo on aina nolla. Toinen ja yksinkertaisempi vaihtoehto käyttää faktorianalyysin tuloksia hyväksi jatkoanalyysissa on muodostaa »summamuuttujat niistä muuttujista, jotka latautuvat vahvasti kullakin faktorilla (eli ns. kärkimuuttujista).

Tilasto-ohjelmistot laskevat tarvittaessa faktoripisteet automaattisesti. Faktoripisteitä voidaan käyttää jatkoanalyysissa joko selittävinä tai selitettävinä muuttujina. Faktoripisteiden käytön havainnollistamiseksi taulukossa 3 on esitetty muutaman vastaajaryhmän sijoittuminen edellisen faktorianalyysin kahdella faktorilla. Tuloksilla on tarkoitus vain konkretisoida esimerkinomaisesti faktoripisteiden käyttömahdollisuuksia. Tarkempi analyysi edellyttäisi selittävien muuttujien huolellista seulontaa sekä havaittujen erojen tilastollisen merkitsevyyden analyysia esimerkiksi »varianssianalyysin tai »regressioanalyysin keinoin. Kannattaa myös huomata, että ’lainkuuliaisuus’ -faktorilla pienet arvot kuvaavat sellaista vastaajaa, joka ei hyväksy laittomia toimia ja suuret arvot vastaajaa, joka on valmiimpi hyväksymään faktorilla latautuneita asioita.

Ryhmä	Keskiarvo ensimmäisellä faktorilla (’Vapaamielisyys’)	Keskiarvo toisella faktorilla (’Lainkuuliaisuus’)
Alle 35-vuotiaat	0,17	0,17
60-vuotta tai yli	-0,43	-0,34

Nainen	-0,01	-0,14
Mies	0,02	0,13

Ei ammatillista koulutusta	-0,15	0,20
Korkeakoulututkinto	0,20	-0,14

Taulukko 3. Valittujen ryhmien faktoripisteiden keskiarvot.

Taulukosta 3 nähdään, että vastaajan iällä vaikuttaisi olevan suuri vaikutus siihen, kuinka he ajattelevat vapaamielisyys-faktorilla latautuvista kysymyksistä. Alle 35-vuotiaat saavat molemmilla faktoreilla suuremmat keskiarvot kuin 60-vuotiaat tai vanhemmat, mikä osoittaa, että he ovat suhteellisesti valmiimpia hyväksymään sekä arvofaktorilla latautuneet asiat että toisella faktorilla latautuneet laittomuudet. Vastaajan sukupuolella ei ole suurtakaan vaikutusta vapaamielisen suhtautumisen yleisyyteen. Sen sijaan toisella faktorilla miesten faktoripisteiden keskiarvo on hiukan suurempi kuin naisten. Miehet ovat siis valmiimpia hyväksymään pikkuvilpin kuin naiset. Myös koulutuksella näyttäisi olevat vaikutusta. Hyvin koulutetut vastaajat ovat vapaamielisempiä kuin vähän koulutusta saaneet. Lainkuuliaisuusfaktorilla keskiarvot ovat päinvastaisia, eli vähän koulutetut ovat vähemmän lainkuuliaisia pikkuvilppiasioissa.

Konfirmatorinen faktorianalyysi

Konfirmatorisen faktorianalyysin lähtökohtana on, että tutkijalla on jo ennen analyysin suorittamista teoriaan perustuva oletus aineiston faktorirakenteesta. Näin konfirmatorinen faktorianalyysi on teorialähtöinen analyysimenetelmä. Sen käyttö edellyttää, että tutkijalla on käytettävissään hyvin muotoiltuja hypoteeseja muuttujien välisistä suhteista ja siitä, kuinka monta faktoria havaitut muuttujat muodostavat. Tämä on lähes päinvastainen lähestymistapa eksploratiiviseen faktorianalyysin verrattuna. Eksploratiivinen faktorianalyysi on luonteeltaan aineistolähtöinen eikä sen käyttö edellytä vahvoja ennakko-oletuksia aineiston faktorirakenteesta.

Käytännössä konfirmatorisen faktorianalyysi edellyttää sitä, että tutkijan on tiedettävä etukäteen, mitkä muuttujat latautuvat milläkin faktorilla ja korreloivatko faktorit keskenään vai ei. Kun faktorit ja niihin kuuluvat muuttujat on valittu, voidaan konfirmatorinen faktorianalyysi toteuttaa. Analyysin tulokset kertovat, miten hyvin alkuperäiset odotukset aineiston faktorirakenteesta pitävät paikkansa. Arviointi perustuu useisiin tilastollisiin tunnuslukuihin, jotka kuvaavat faktorimallin soveltuvuutta aineistoon.

Rakenneyhtälömallit (structural equation models) ovat eräänlainen konfirmatorisen faktorianalyysin laajennus. Niissä yhdistyvät sekä faktori- että »regressioanalyysi. Hieman yksinkertaistettuna rakenneyhtälömallien ideana on tarkastella regressioanalyysin avulla faktorien välisiä kausaalisuhteita. Tutkimuksessa on esimerkiksi voitu muodostaa faktorianalyysin avulla vastaajien masentuneisuutta ja itsetuntoa koskevat faktorit. Rakenneyhtälömallien avulla voidaan tutkia, minkälainen kausaalinen vaikutus itsetunnolla on masentuneisuuteen.

Useimpien yleiskäyttöisten tilastoanalyysiohjelmien perusmodulit eivät sisällä konfirmatoriseen faktorianalyysiin ja rakenneyhtälömallien analysointiin tarkoitettuja työkaluja. Esimerkiksi SPSS-tilasto-ohjelman yhteydessä käytetään AMOS-nimistä konfirmatoriseen faktorianalyysiin erikoistunutta ohjelmaa, joka täytyy hankkia erikseen. ’Lisätietoja’-osuudessa on linkkejä eri ohjelmiin, joilla konfirmatorisia faktorimalleja ja rakenneyhtälömalleja voidaan toteuttaa.

Lisätietoja

Faktorianalyysista on saatavilla runsaasti suomenkielistä materiaalia. Seuraavassa listassa Nummenmaan ym. kirja käsittelee faktorianalyysia kaikkein perusteellisimmin. Lisäksi siinä esitellään myös konfirmatorista faktorianalyysia ja rakenneyhtälömalleja.

Alkula, Tapani & Pöntinen, Seppo & Ylöstalo, Pekka (1994): Sosiaalitutkimuksen kvantitatiiviset menetelmät. WSOY, Juva.
Karma, Kai & Komulainen, Erkki (1992): Käyttäytymistieteiden tilastomenetelmien jatkokurssi. Yliopistopaino, Helsinki.
Nummenmaa, Tapio & Konttinen, Raimo & Kuusinen, Jorma & Leskinen, Esko (1996): Tutkimusaineiston analyysi. WSOY, Porvoo.
Toivonen, Timo (1999): Empiirinen sosiaalitutkimus: filosofia ja metodologia. WSOY, Porvoo.

Englanniksi faktorianalyysia esitellään hyvin seuraavissa kirjoissa. De Vausin kirja sopii parhaiten aloittelijalle. Tabachnickin ja Fidellin kirja menee esittelyssään syvemmälle. Siinä käsitellään sekä eksploratiivista että konfirmatorista faktorianalyysia.

De Vaus, D.A. (1994): Surveys in Social Research. Third edition. UCL Press, Guildford.
Tabachnick, Barbara G. & Fidell, Linda S. (1996): Using Multivariate Statistics. Harper Collins, New York.

Verkosta löytyy paljon faktorianalyysia käsittelevää materiaalia. Richard B. Darlington Cornellin yliopistosta on kirjoittanut hyvän aloittelijoille sopivan esittelyn faktorianalyysista. Se löytyy osoitteesta:

· http://comp9.psych.cornell.edu/Darlington/factor.htm

Myös Colleen Flynn Thapalia on kirjoittanut lyhyen esittelyn faktorianalyysista. Se löytyy osoitteesta:

· http://trochim.human.cornell.edu/tutorial/flynn/factor.htm

Connie D. Stapleton on tuottanut hyvän esittelyn konfirmatorisesta faktorianalyysista. Osoite on:

· http://ericae.net/ft/tamu/Cfa.HTM

David Garsonin ”Statnotes: an Online Textbook” on oivallinen lähde sekä faktorianalyysiin että rakenneyhtälömalleihin liittyvissä asioissa. Osoitteet ovat:

· Faktorianalyysi: http://www2.chass.ncsu.edu/garson/pa765/factor.htm

· Rakenneyhtälömallit: http://www2.chass.ncsu.edu/garson/pa765/structur.htm

Yleisesti konfirmatorisesta faktorianalyysista ja rakenneyhtälömalleista kerrotaan SEM FAQ sivuilla (SEM = Structural Equation Models) osoitteessa:

· http://www.gsu.edu/~mkteer/semfaq.html

Konfirmatorisessa faktorianalyysissa ja rakenneyhtälömalleissa yleisesti käytettyjä ohjelmia ovat:

· AMOS: http://www.smallwaters.com/

· EQS: http://www.mvsoft.com/

· LISCOMP: http://www.gsu.edu/~mkteer/liscomp.html

· LISREL: http://www.ssicentral.com/lisrel/mainlis.htm

Kalvot

o Joidenkin käsitteiden mittaaminen yhdellä muuttujalla mahdotonta

o tarvitaan useita samaa ilmiötä mittaavia muuttujia

o Faktori on piilevä, ei suoraan havaittavissa oleva, konstruktio, jonka olemassaolo päätellään mitattavissa olevista muuttujista

o Esimerkkejä faktoreista: konservatiivisuus, sosiaalisuus, vieraantuminen, älykkyys

o Faktoreita tutkitaan faktorianalyysin avulla

o Eksploratiivinen faktorianalyysi

o Aineistolähtöinen menetelmä

o Ei vahvoja etukäteisoletuksia faktoreiden määrästä tai niihin liittyvistä muuttujista

o Konfirmatorinen faktorianalyysi

o Teorialähtöinen menetelmä

o Tutkijalla etukäteen hypoteesit faktorirakenteesta

o Faktorianalyysin perusidea

o Kuvio 1

o Faktorilataukset kuvaavat havaittujen muuttujien ja faktorin yhteyden vahvuutta

o Saavat arvoja –1 ja 1 välillä

o Mitä lähempänä faktorilatauksen itseisarvo on yhtä, sitä voimakkaammin havaittu muuttuja latautuu faktorilla

o Ominaisarvot kuvaavat sitä, kuinka hyvin faktorit pystyvät selittämään havaittujen muuttujien vaihtelua

o Jatkoanalyysiin otetaan yleensä vain sellaiset faktorit, joiden ominaisarvo on yhtä suurempi (>1)

o Kun ominaisarvo jaetaan muuttujien määrällä saadaan faktorin selitysosuus

o Mitä suurempi selitysosuus on, sitä paremmin pystyvät faktorit kuvaamaan aineiston rakennetta

o Kommunaliteetit kertovat, kuinka suuri osuus havaittujen muuttujien vaihtelusta pystytään selittämään kaikkien faktoreiden avulla

o Mitä lähempänä yhtä (1) kommunaliteetti on, sitä paremmin faktorit selittävät muuttujan vaihtelua

o Jos muuttujan kommunaliteetti on pieni, kannattaa harkita sen pudottamista pois analyysista

o Rotaation avulla faktorilatausten saadaan tulkinta yksinkertaisemmaksi

o Rotaatiolla tarkoitetaan faktoriakselien ”kiertämistä” siten, että faktorirakenne tulee selkeämmäksi

o Kaksi eri lähestymistapaa: suorakulma- ja vinokulmarotaatio

o Esimerkkifaktorianalyysi

o Taulukko 2

o Faktoripisteet kuvaavat yksittäisten havaintojen sijoittumista faktoreilla

o Voidaan käyttää jatkoanalyysissa joko selitettävinä tai selittävinä muuttujina

o Muuttujista voidaan myös muodostaa summamuuttujia faktorianalyysin tulosten pohjalta

o Konfirmatorinen faktorianalyysi

o Lähtökohtana teoriaan perustuva oletus aineiston faktorirakenteesta

o Etukäteishypoteesit faktorien määrästä ja niillä latautuvista muuttujista

o Analyysin tuloksien avulla voidaan arvioida, kuinka hyvin oletukset pitivät paikkansa