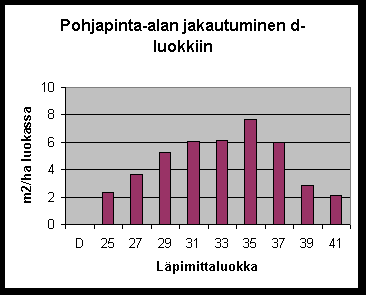
Kuivajärven luonnonhoitometsässä sijaitsevaa kuusikkokoealaa 112 käytetään seuraavassa esimerkkinä puuston kokojakaumaa käsiteltäessä. 115-vuotiaasta kuusikosta on tehty runkolukusarjan mittaus ja tulokset esitetään alla taulukossa 2 cm-luokissa:

Runkolukusarja:

d r/ha G/lk    %
25 48 2.356 0.055
27 64 3.664 0.086
29 80 5.284 0.125
31 80 6.038 0.143
33 72 6.158 0.146
35 80 7.696 0.182
37 56 6.021 0.142
39 24 2.867 0.067
41 16 2.112 0.050

- r/ha-sarakkeesta ilmenee, kuinka monta kyseiseen lpm-luokkaan kuuluvaa puuta koealalla on /ha.
- G/lk -sarakkeesta ilmenee, kuinka monta neliömetriä pohjapinta-alaa / ha kyseisessä lpm-luokassa on.
- %-sarakkeesta ilmenee, mikä on kyseisen luokan osuus kokonaispohjapinta-alasta.
- kuvaan on piirretty ppa-läpimittajakauma, eli G/lk-sarakkeen tiedot.

Koeala 112 tiedot ovat vuodelta, jolloin koealan puusto (kuusikko) oli 115-vuotiasta, pohjapinta-ala 42.2 m2/ha ja keskiläpimitta 33 cm.

Runkolukusarjan mittaaminen jokaisesta metsiköstä on aikaaviepää. Herääkin kysymys, voisiko tätä työtä kenties helpottaa, jos löydetään joitakin helpommin mitattavia/arvioitavia tekijöitä, joiden avulla runkolukusarjan (eli puuston kokojakauman) voisi ennustaa ja laskea ilman, että jokaisen puun läpimittaa tarvitsisi mitata?

Tarvitaan matemaattinen jakautumismalli, jolla ennustaa havaittuja jakaumia. Otetaan käyttöön Weibullin jakauma G/luokka ~Weibull(a,b,c), koska se on jakauma, joka tarvittaessa 'säätyy' symmetrialtaan vinoksi, on helppo käsittellä laskennallisesti, ja jonka parametrit (Weibullin tapauksessa a,b,c) on laskettavissa / ennustettavissa empiirisestä aineistosta.

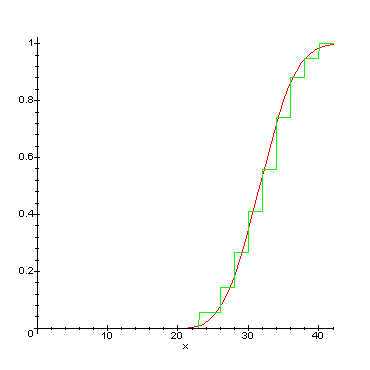
Lasketaan esim. vuoksi Weibull-tiheysfunktion parametrit a,b,c koealan 112 puuston kokojakaumalle:

Parametrien a, b ja c oikeiden arvojen löytämiseksi on useita menetelmiä, joista tässä on käytetty ns. prosentti-osuus menetelmää.

Kuvaan on piirretty Pohjapinta-alan kertymäfunktiot. Porrasfunktio kuvaa mitatuista läpimitoista laskettua summafrekvenssiä, ja jatkuva funktio on prosenttimenetelmällä estimoidun Weibull-funktion (kertymäfunktion) kuvaaja. Y-akseli kuvaa, kuinka paljon pohjapinta-alaa kertyy läpimitan kasvaessa (prosentuaalisesti).

Parametriestimaattien numeroarvot ovat prosenttimenetelmällä estimoiden (kts. Silva carelica 17 s. 49)

a = 20 (cm), b = 13 ja c = 3.3.

Parametri a kuvaa jakauman sijaintia (minimiläpimitta), b skaalaa jakaumaa ja c määrää sen muodon (symmetrinen, vino vasemmalle tai oikealle).
Parametrit a, b ja c voitaisiin määritellä/laskea kaikille 88 kuusikkokoealalle, joista vuosina 1975-1995 on kertynyt tietoa puuston läpimitta(koko)(pohjapinta-ala) -jakaumasta.

Sitten laadittaisiin mallit a,b ja c:lle käyttäen selittävinä muuttujina mm. metsikön ikää, keskiläpimittaa, pohjapinta-alaa, ja vaikka puulajin puulajiosuutta. Nämä muuttujathan tunnetaan kaikille mittauskerroille.

 

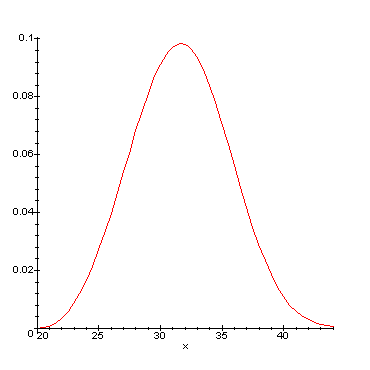
Parametriarvoilla a = 20 (cm), b = 13 ja c = 3.3.

weibull-tiheysfunktio näyttää tältä.

Tiheysfunktio kertoo, kuinka paljon pohjapinta-alaa kullekin läpimittajakauman osalle 'osuu'. Tiheysfunktiota integroimalla (laskemalla pinta-alaa, joka jää käyrän ja x-akselin väliin) saadaan ylle kuvattu kertymäfunktio, joka antaa kokonaispohja-pinta-alan arvoksi 1 (100 %). Kertymäfunktiota voidaan integroida myös paloittain, jolloin saadaan esim. välin 20-25 cm ppa-osuus.

(x-akselilla on siis läpimitta).

Kuinka näitä Weibull-malleja sitten käytetään ?

Kuvitellaan tilanne, jossa 'arviointimies' mittaa kuvioittaisen arvioinnin yhteydessä metsikkökuviota, joka on koelan 112 kaltainen. Sen sijaan, että hän kaivaisi lpm-saksia repustaan ja ryhtyisi mittailemaan läpimittasarjoja, hän tyytyy arvioimaan keskiläpimitan, keskipituuden, iän, pohjapinta-alan (relaskoopilla) ja kuusen osuuden puustosta. Tästä hän suoriutuu muutamassa minuutissa.

Arvot, jotka piirtyvät lomakkeelle ja syötetään tietokoneelle ovat: D 34 cm, T 120 v, G 42 m2/ha ja kuusta 100 % (PPC).

Tietokoneeseen on ohjelmoitu mallit a,b ja c:lle Weibullin jakaumaa varten (mallit on laskettu Valtakunnan Metsien Inventointi -aineistosta, ei Hyytiälän aineistosta).

a:= 0.7275+0.003988*D^2-0.00008*T^2+0.001767*PPC;
c:= exp(0.7072+0.03263*D-0.1518*ln(T)+0.002367*PPC);
b:= (D-a)/(-ln(0.5))^(1/c);

Arvot ovat malleilla laskien a= 2.34, b= 34.88, c= 3.76.

Niillä piirretty pohjapinta-alan jakauma ja kertymäfunktio alla:

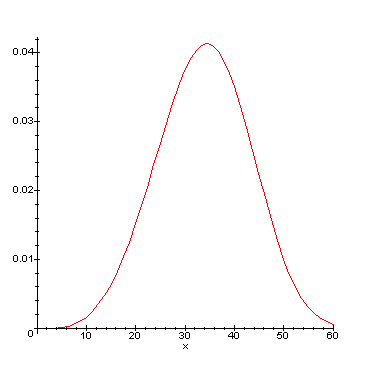
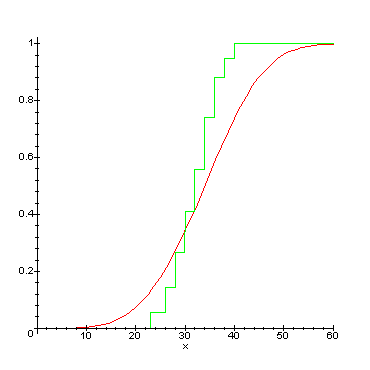
Koealalta mitattu pohja-pinta-alan kertymäfunktiota (porrasfunktio) ja mallilla laskettua matemaattista kertymäfunktiota silmäillessä huomaa, ettei VMI-aineistosta laadittu malli kovin hyvin osaa ennustaa koealan n:o 112 puuston jakautumista kokoluokkiin. Malli ennustaa läpimittojen alkavan jo 6 cm:stä ja jatkuvan aina n. 60 cm:iin puihin saakka. Sen sijaan empiirisessä aineistossa läpimittoja havaittiin vain välillä 24 - 43 cm!

Hyytiälän kuusikoille on siis syytä laatia oma malli, koska valtakunnallisen mallin ennusteet näyttävät huonoilta (huom! päätelmä huonoudesta tehdään nyt vain yhden tutkitun kuusikon perusteella).

Kuviteellaan, että sellainen pystytään laatimaan 88 koealan pohjalta ja se antaa yhdistelmälle D 34 cm, T 120 v, PPC 100 % kuusta parametriarvot a 19.9, b 13.1 c 3.3. Esimerkki ontuu, sillä aluksi laskimme juuri näitä parametreja lähellä olevat 'hyvät' luvut koealalle 112

Weibull-tiheysfunktio on (x vastaa läpimittaa):

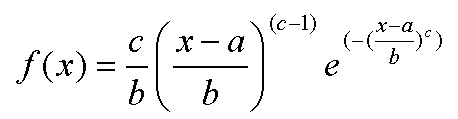
ja integraalifunktio

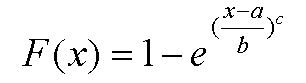
Integroidaan tiheysfunktio 2 cm luokissa, 20..22, 22..24, 24..26 jne. , jolloin saamme kunkin 2 cm:n luokan pohjapinta-alaosuudet selville. Eli sijoitetaan annetut a,b ja c integraalikaavaan ja lasketaan x:n arvoilla 20..22, 22..24 jne.

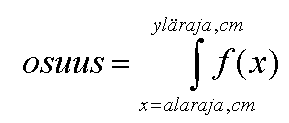
Tulokset alla:

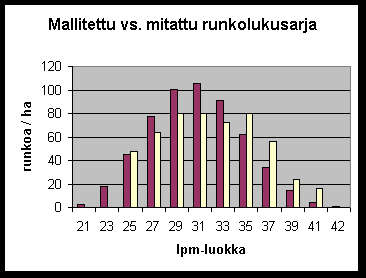
       ppa-osuus runkoluku
d  malli mitattu malli mitattu
21 0.002 0.000     2     0
23 0.018 0.000    18     0
25 0.053 0.055    45    48
27 0.105 0.086    77    64
29 0.158 0.125   100    80
31 0.190 0.143   106    80
33 0.185 0.146    91    72
35 0.143 0.182    62    80
37 0.087 0.142    34    56
39 0.040 0.067    14    24
41 0.014 0.050     4    16
42+ 0.004 0.000    1     0

Jos kuvitteellinen mallimme onnistuisi todellisuudessa ennustamaan kuvan mukaisella tavalla runkolukusarjan useimmissa tapauksissa, voisi mallia sanallisesti kuvata 'hyväksi'. Esimerkissä parametreja ei saatu millään todellisella mallilla, vaan niiden likiarvot laskettiin yhden koealan aineistosta.

On selvää, että lpm-jakauman muotoon vaikuttaa seikkoja, joita muutujat D, T, G ja puulajin osuus eivät kuvaa. Soilla ja kankailla runkolukusarjat kehittyvät luontaisesti erilaisiksi. Valtion, yritysten ja yksityisten metsänomistajien metsiä hakataan ja hoidetaan eri periaattein, ja ne periaatteet eivät kokonaan kuvaudu selittävien muuttujien kautta. Maantieteellinen sijainti saattaisi myös olla merkittävä luontaisen vaihtelun aiheuttaja.

Nyt meillä on kuitenkin mallitettu estimaatti sille, kuinka puut jakautuvat kokoluokkiin metsikössä, josta tätä varten mitattiin vain D, T, G ja puulajiosuus.

Jos edelleen tiedämme, kuinka pituudet puille määräytyvät (pituusmalli), voimme esim. harventaa metsää tietokoneella (simuloida hakkuun), ja laskea harvennuskertymän puutavaralajeittain käyttäen apuna puutason runkokäyrämalleja, jotka laadittiin ensimmäisenä (tosin esimerkeissä 1,2,3 männylle).

Tulevaisuutta ennustettaessa voimme käyttää metsikkötason kasvumallien sijaan (esimerkki) yksittäisen puun kasvua ja kehitystä ennustavia malleja, koska kokojakauman avulla pääsemme aina puutasolle saakka. Metsikkökoealoilta, joissa puut tunnetaan ja niiden kehitystä seurataan, muodostavat aineiston tälläisten yksittäisen puun kehitystä kuvaavien mallien laatijoille.