
Kuvaan vas. on piirretty eräs metsikkökovio puineen ja kuviorajoineen. Ympyrän halkaisija kuvastaa korostetustu puun läpimittaa, eikä ole samassa mittakaavassa kuin kuvioraja. Kuvion pinta-ala on noin 0.7 ha
Jos tavoitteena on selvittää tämän kuvion puustotunnukset tarkasti, se kannattaa tehdä s.e. mittaa tarkasti jokaisen puun puutunnukset. Tehdään ns. 'täysluku'. Jokaisesta puusta mitataan esim. puulaji, d, d6 ja h.
Kuinka lähellä oikeaa arvoaan saadut tulokset tällöin
ovat ?
Tähän vastatakseen pitää ensin täsmentää
joitakin yksityiskohtia ja varmistaa muutama asia.
Täsmennystä kaipaa mm. se, minkälainen metsikkö on kyseessä, sillä tarkkusarvion antamiseksi pitää tietää, onko kyseisen metsikön puulajeille ja kyseisellä alueella laadittu puumalleja, vai pitääkö kenties tyytyä tarkkuudeltaan karkeampaan relaskooppitaulukkoon tms., ja mikä on malleille luvattu tarkkuus. Lisätietona on hyvä myös olla selvillä mittausten hyvyydestä. Mikä instrumentti esimerkiksi on käytössä, kun pituuksia tai yläläpimittoja mitataan, sillä instrumenttien välillä on tarkkuuseroja. Samoin kokonaistarkkuusarvion antajaa kiinnostaa tieto mittaajien ammattitaidosta, osaavatko he käyttää laitteita, ja ovatko he ylipäänsä huolellisia?.
Mallivirhe jää jäljelle, kun metsikkö mitataan puu kerrallaan, kaikista puista luetaan tarvittavat tunnukset (kaikki puut ovat koepuita) ja mittaus oletetaan tehdyksi absoluuttisen tarkasti. Mallivirhe on parhaimmillaan sellaista, että jollekin puulle mallin antama yliarvio korvautuu toiselle puulle tulleesta aliarviosta. Usein kuitenkin esim. metsikössä on 'jotain', jonka takia mallivirheet eivät kumoudukaan. Poikkeuksellinen metsänhoito tai muu toimenpide on 'kohdannut' kaikkia metsikön puita. Mallivirheestä harvoin päästään kokonaan eroon, ja systemaattista virhettä pitää kontrolloida kalibroinnein ja kontrollein.
Kts. esimerkin 6 pistekuvia, niissä mallivirhe kuvattuna.
Mittausvirhettä syntyy aina. Tähän luokkaan voi lukea myös mittauksen yhteydessä syntyneet muut inhimilliset virheet, kuten kirjoitusvirheet. Mitattava kohde monasti vaikuttaa tämän virhekomponentin suuruuteen. Esim. pituusvirhe on minimissään, kun luetaan 45 asteen kulmassa hypsometrillä tms. laitteella (kts. kuva ja esimerkki alla). Suuripuustoisissa kohteissa ei jakseta kävellä 45 asteen katselukulman etäisyydelle. Tässäkin tapauksessa systemaattiset virheet ovat pahimpia ja niiden syntymistä tulisi välttää. Huono mittaus voi olla viisaampaa jättää tekemättä, jos siinä tehtyjen virheiden vaikutus kumoaa mittausten tuloksia tarkentavan vaikutuksen. Tästä esimerkki ovat huonot yläläpimittamittaukset, jotka pahimmillaan huonontavat yksittäisen puun tilavuusarviota.
Hypsometrin periaate (tässä silmä on puun tyven tasolla), esimerkki mittausvirheen syntymisestä:
Puun pituus = katseluetäisyys(x) * tan(kulma(a))
![]()
Muutos pituudessa sh, kun hypsometri värisee kädessä vakiokulman sa verran. Ratkaistaan
ositt. derivoimalla kulman aja etäisyyden x suhteen . Kaava, jolla voi arvoidaan virheen maksimisuuruuden itseisarvo on:
![]()
Oletetaan, että s x on nolla (oletetaan siis, että mittaaja pysyy vakioetäisyyden päässä, eikä siis huoju tai liiku mitatessaan). Tällöin pituuden muodostuu virhe kulman pituuden osittaisderivaatasta kulman a suhteen ja kulman muutoksesta delta sa.
![]()
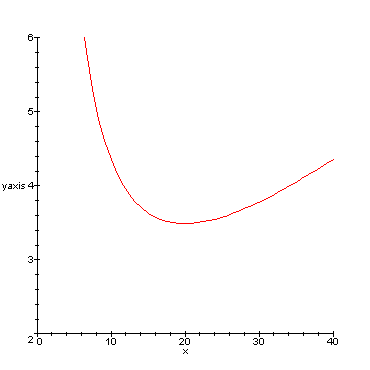 Jos oletetaan, että
värinä hypsometrissä on vakiokulmaista, eli hypso esim.
vaappuu ±5 astetta ja mitataan 20 metriä pitkää puuta,
muodostuu tästä aiheutuva virhemaksimin kuvaaja etäisyyden
x suhteen alla olevan kaltaiseksi:
Jos oletetaan, että
värinä hypsometrissä on vakiokulmaista, eli hypso esim.
vaappuu ±5 astetta ja mitataan 20 metriä pitkää puuta,
muodostuu tästä aiheutuva virhemaksimin kuvaaja etäisyyden
x suhteen alla olevan kaltaiseksi:
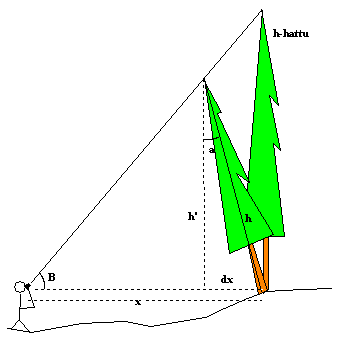
Vakiotärinä ±5 astetta aiheuttaa siis pahimmillaan esim. 10 metrin etäisyydeltä n. ± 4.4 metrin virheen pituuteen, 20 metrin etäisyydeltä enää ± 3.6 metrin virheen, ja 40 metrin päästä 20 metriä pitkää puuta ± 4.3 metrin pituusvirheen.
Nämä arviot ovat siis pahimmille virheitä, joita syntyy kun hypsometrin asteikko vaappuu tuon ± 5 astetta.
Todelliset virheet asettuvat jonnekin ± mainittujen maksimiarvojen väliin, ja niiden jakauma voi olla esim. normaalijakauman muotoista. Jakauman muoto ja sijainti riippuu siitä, millä kohtaa tärinää mittaaja yleensä havaitsee 'mittauslukeman'.
Kuvaaja todistaa ns. vakiokulmamenetelmän puolesta puun pituutta mitattaessa.
Pohditaanpa, millaisen muotoiseksi virhejakauma voisi muodostua:
 Kuva koetilanteesta.
Kuva koetilanteesta.
Ylälukemaa luettaessa luettaessa hypsometri mittaajan kädessä 'vaappuu' s.e. asteikkokiekko hypsometrin sisällä tekee ± # asteen liikettä. Oletetaan yksinkertaisuuden vuoksi, että hypsometri ei liiku, ainoastaan asteikko sen sisällä. Heilunta on (heiluriperiaate) sellaista, että liike pysähtyy aina, kun sen suunta kääntyy ja nopeus on suurimmillaan, juuri, kun oikea lukema olisi kohdalla.
a) Oletetaan, että mittaajalla on ilmiömäinen kyky 'pysäyttää heilurin liike' ja ottaa siitä lukema kyseisellä ajanhetkellä. Mittaaja ei kuitenkaan tiedä, milloin hänen pitäisi lukema ottaa, joten hän päättää satunnaistaa tuon hetken. Hän siis pysäyttää liikkeen äärettömän nopealla silmällään, ja lukee lukeman satunnaisella ajanhetkellä. Todennäköisyys sille, mistä kohtaa heilurin liikettä mittaushavainto tulee, riippuu siis siitä, mikä on heilurin nopeus kussakin paikassa. Tästä syystä havainnot painottuvat liikkeen ääripäihin, joissa heiluri 'viettää aikaa' pysähtyneenä ja kiihtyvässä hitaassa liikkeessä. Sen sijaan oikean arvon kohdalta havaintoja tulee vähemmän, koska siinä vauhti on suurimmillaan. Virheiden jakaumasta tulee alla olevan kuvan kaltaista.
b) Oletetaan edelleen, että mittaajalla on inhimillinen tapa nähdä todennäköisemmin lukemia silloin, kun heilurin liike on hitaimmillaan, mutta havaintoa tehdessään hän tekee aina kaksi havaintoa asteikolta, ja ilmoittaa tulokseksi niiden keskiarvon. Näiden tulosten jakauma ei enää keskity havaintojen laidoille, vaan nyt jakauma alkaa normalisoitua keskiarvoistamisen takia.
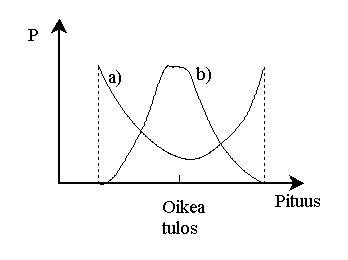
Tapausten a) ja b) mukaiset mittausvirheiden jakaumat.
Tapaus a) pätee mm. silloin, kun käytössä on ns. Blume-Leiss -hypsometri. Tässä hypsometrityypissä on käytössä heiluri, jonka liike pysäytetään laukaisemalla liipasimesta.
Tarkkaavainen lukija on jo varmaan huomannut, että tarkastelumme
on ollut puutteellista. Emme ole lainkaan tutkineet, kuinka ns. alalukeman
virheet s.o. mittaushavainto puun tyvelle, käyttäytyy.
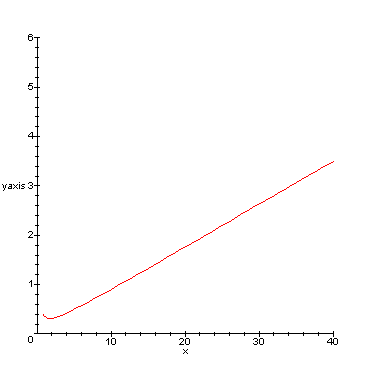
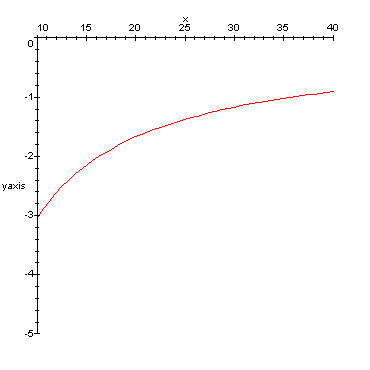
Kuvaaja alalukeman maksimimittausvirheelle (sen itseisarvolle) etäisyyden
funktiona.
Kuvaajaa piirrettäessä on oletettu, että silmä
on 180 cm korkeudella puun tyveen nähden (minimi, koska silloin 45
kulmassa tähtäys tyvelle).
Tämä virhekomponentti on siis lähes lineaarisesti etäisyydestä
riippuva silloin, kun oletetaan, että hypsometrin sisällä
asteikkokiekko tekee vakiokulmaista heiluriliikettä.
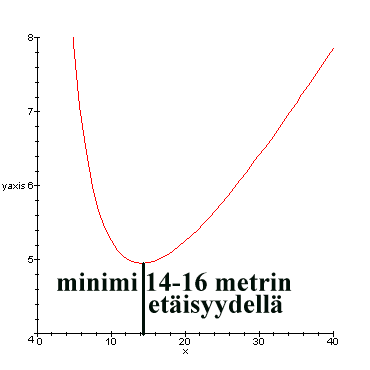 Kun nämä kaksi
virhekomponenttia lasketaan yhteen, saadaan kokonaismittausvirheen itseisarvolle
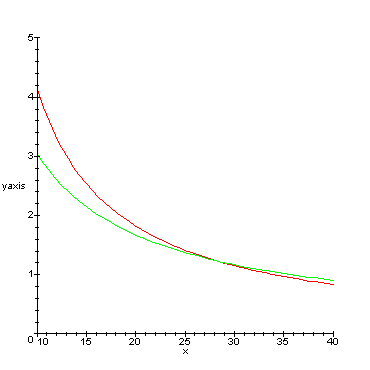
teoreettinen maksimi (kuva).
Kun nämä kaksi
virhekomponenttia lasketaan yhteen, saadaan kokonaismittausvirheen itseisarvolle
teoreettinen maksimi (kuva).
Kuvasta voi havaita, että 20-metristä puuta mitattaessa maksimivirhe minimoituu, kun puuta siis katsellaan 180 cm sen tyven yläpuolelta ja n. 14-16 metrin etäisyydeltä.
Jos oletukset mittausvirheen luonteesta pitävät paikkansa, ja puut seisovat pystyssä sillä etäisyydellä (x), jolla niitä katsellaan, kannattaa hypsometrillä mitata 20-metrisiä puita noin 15 metrin etäisyydeltä.
Entäpä jos puut ovat kalleellaan, joskus mittaajaa kohti, ja joskus poispäin? Onko tällöinkin edelleen järkevää mitata yli 45 asteen katselukulmalla?
Oletetaan, että kyseinen 20-metrinen puu on 5 astetta kallellaan kohti katsojaa.
Virhe, jonka puun kallistuma aiheuttaa, riippuu toisaalta puun pituudesta (kiinnitetty: 20 m), itse kallistumasta (kiinnitetty: 5 astetta), ja sen suunnasta (kiinnitetty: kohti mittaajaa) ja etäisyydestä, jolta puuta mitataan (annetaan vaihdella). Oletetaan nyt mittaus tehtävän tarkkana, ilman, että asteikkokiekko hypsometrin sisällä heiluisi.
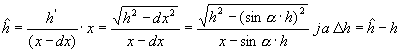
h-hattu on arvio pituudelle, h' on pituuden pystysuora komponentti (kuva),
dx on kallistuman aih. virhe latvan etäisyydelle, a
on kallistuskulma ja h puun todellinen pituus (kts. kuva).
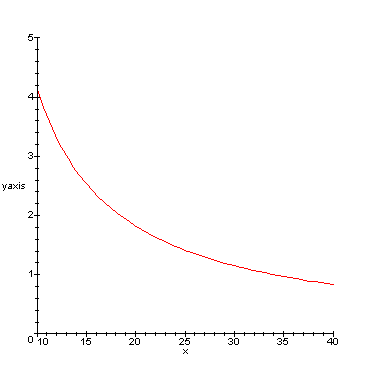
Kallistuma kohtimittaajaa aiheuttaa tulokseen yliarvion, jonka suuruus pienenee mittausetäisyyden kasvaessa. Tämä seikka puoltaisi pidempää kuin 14-16 metrin katseluetäisyyttä, johon ed. tarkastelussa päädyttiin (puun todellinen pituus 20 metriä).
Jos puu taasen on kallistunut poispäin mittajasta, aiheutuu tuloksiin aliarvio, joka käyttäytyy mittausetäisyyden funktiona (10-40 m):
Jos puun mittaussuunta valitaan satunnaisesti, niin tällöin mittaajaan päin ja mittaajasta poispäin olevia puita on periaatteessa yhtä paljon.
 Huomaa virhekuvioita tarkastellessasi,
etteivät yli- ja aliarviot todelliselle pituudelle ole itseisarvoltaan
yhtä suuria samalle mittausetäisyydelle: Kun puu on kallistunut
kohti mittaajaa, aiheutuu siitä suurempi virhe, kuin saman kallistuskulman
verran mittajasta poispäin olevan puun pituudelle. 20 metrisen puun
tapauksessa virheet ovat itseisarvoltaan yhtäsuuria n. 28 metrin mittausetäisyydellä.
Huomaa virhekuvioita tarkastellessasi,
etteivät yli- ja aliarviot todelliselle pituudelle ole itseisarvoltaan
yhtä suuria samalle mittausetäisyydelle: Kun puu on kallistunut
kohti mittaajaa, aiheutuu siitä suurempi virhe, kuin saman kallistuskulman
verran mittajasta poispäin olevan puun pituudelle. 20 metrisen puun
tapauksessa virheet ovat itseisarvoltaan yhtäsuuria n. 28 metrin mittausetäisyydellä.
Tämä merkitsee sitä, että hypsometrilla tapahtuvissa pituusmittauksissa on aina harhaa, jos puiden kallistumia ei mitata (epälineaarisuutta, epäsymmetrisyyttä).
Vai onko näin sittenkään? Entäpä, jos puut ovat myös sivusuunnassa kallellaan? Tällöin vaikuttaisi siltä, että pituudet tulevat systemaattisesti aliarvioiduiksi. Kompensoisiko tämä ilmiö edellisestä aiheutuvan positiivisen harhan?
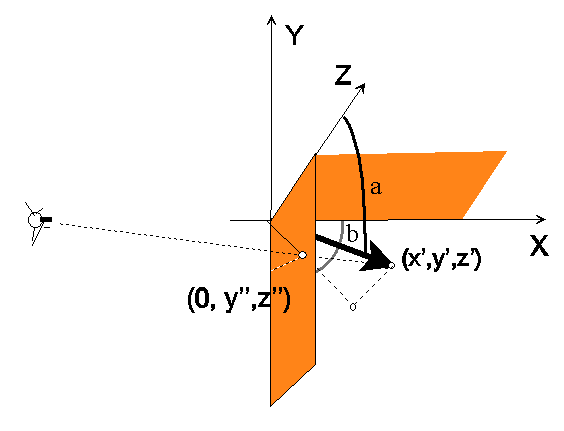 Tarkistellaanpa tilannetta
kahden kulman ((a) sivu- ja (b) kiertokallistuksen suhteen) ja yläilmoista:
Tarkistellaanpa tilannetta
kahden kulman ((a) sivu- ja (b) kiertokallistuksen suhteen) ja yläilmoista:
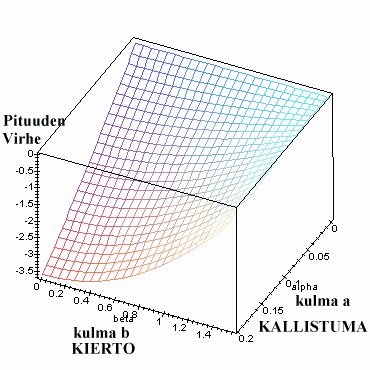 Kuvassa
XY-taso vastaa maanpintaa. X-akseli sijoittuu linjalle mittaaja-puu, ja
Y-akseli tähän nähden kohtisuoraan. Puu on kallistunut poispäin
mittaajasta. Kallistuma pois pystysuorasta suunnasta on kulman a suuruista
ja kiertymä x-akselin suhteen on kulman b suuruinen. Kuinka mittausvirhe
käyttäytyy kulmien a ja b funktiona. Oletetaan jälleen 20-metrinen
puu ja absoluuttisen vakaa mittakäsi (ja silmä).
Kuvassa
XY-taso vastaa maanpintaa. X-akseli sijoittuu linjalle mittaaja-puu, ja
Y-akseli tähän nähden kohtisuoraan. Puu on kallistunut poispäin
mittaajasta. Kallistuma pois pystysuorasta suunnasta on kulman a suuruista
ja kiertymä x-akselin suhteen on kulman b suuruinen. Kuinka mittausvirhe
käyttäytyy kulmien a ja b funktiona. Oletetaan jälleen 20-metrinen
puu ja absoluuttisen vakaa mittakäsi (ja silmä).
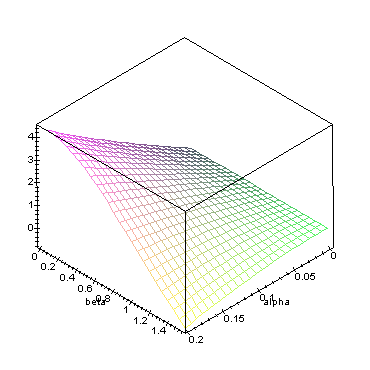
Kuvassa vas. aliarvion käyttäytyminen kun puu on kallellaan samassa koordinaattineljänneksessä kuin yllä olevassa lintuperspektiivikuvassa. Kuvaa piirrettäesssä on kallistuskulman annettu vaihdella 0-11.45 astetta ja kiertokolman 0...90 astetta. Oikea kuva vastaa tilannetta, jossa puu on kallistunut kohti mittaajaa 0-11.45 astetta ja kiertokulman annetaan liikkua arvosta 'suoraan kohti' arvoon 'suoraan sivulle'.
Poispäin: Pahin virhe, -3.5 metriä aiheutuu silloin, kun puu on kallellaan täydet 11.45 astetta suoraan mittaajasta poispäin (kierto on nolla). Kun puu on suorassa, saadaan oikea tulos kierrosta riippumatta (laatikon takaseinä) ja kun puu on täydet 11.45 astetta kallellaan, mutta suoraan sivulle, saadaan 40 cm aliarvio. Oletus: puu on 20 metriä pitkä ja mittausetäisyys 20 m.
Kohti mittaajaa: Pahin virhe +4.0 metriä.
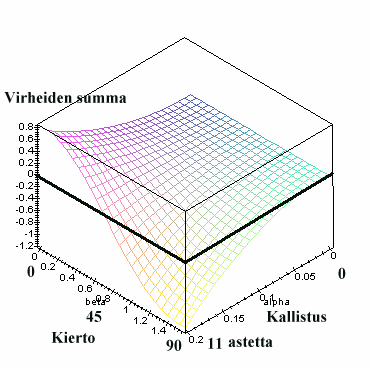 Virheiden summa kertoo,
kuinka eri kallistuskulmilla ja kierroilla virheet kompensoivat toisiaan.
Jos pinnan keskikorkeus on nolla, ovat tulokset keskimäärin harhattomia.
Pohdi onko se?
Virheiden summa kertoo,
kuinka eri kallistuskulmilla ja kierroilla virheet kompensoivat toisiaan.
Jos pinnan keskikorkeus on nolla, ovat tulokset keskimäärin harhattomia.
Pohdi onko se?
Jos oletetaan, että puiden kallistuskulma (a) on tasajakautunut välille 0-11.45 astetta ja puita katsellaan satunnaisesta suunnasta, jolloin myös kierto b on tasajakautunut välille 0-360 astetta, mittausetäisyys on 20 metriä ja puun pituus 20 metriä, ovat tulokset keskimäärin - 3.4 mm harhaisia. Jos sen sijaan oletamme, että 20 -metristen puiden kallistuskulmat jakautuvat siten, että suoria puita on enemmän, ja yhä vähemmän kallellaan olevia yhä vähemmän (kuva alla), pienenee harha arvoon -0.2 mm (laskettu 18000 simuloidulla havainnolla). Onko harhalla merkitystä?
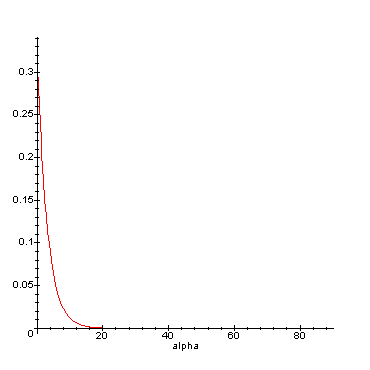 Vas. kallistuskulmien oletettu
eksponentiaalijakauma. Odotusarvo 3 astetta. Todennäköisyys sille,
että kallistus on yli 10 astetta on pieni, alle 4 %.
Vas. kallistuskulmien oletettu
eksponentiaalijakauma. Odotusarvo 3 astetta. Todennäköisyys sille,
että kallistus on yli 10 astetta on pieni, alle 4 %.
Sellainen havainto voidaan vielä tehdä, että jos pituus mitataan 1.4142 (neliöjuuri 2) kertaa puun pituuden etäisyydeltä, kallistumisesta ei aiheidu harhaa tuloksiin!
Kiinnitetään vielä pituusmittausvirheen merkitys johonkin johdettuun suureeseen. Oletetaan, että olimme alunperin kiinnostuneita kyseisen 20-metrisen puun runkotilavuudesta. Puun läpimitta on 24 cm ja sen osaamme mitata tarkasti. Oletetaan, että pituutta mitataessa tehdään 'asteikon heiluriliikkestä' johtuvaa mittausvirhettä, puu seisoo suorassa, ja mittausvirhe oletetaan normaalijakautuneeksi odotusarvonaan nolla metriä ja keskihajontana 1.0 m. Tilavuuden laskemiseksi käytämme Laasasenaho tilavuusyhtälöä kuuselle: v = 0.022927* d^1.91505 * 0.99146^d * h^2.82541 * (h-1.3)^-1.53547
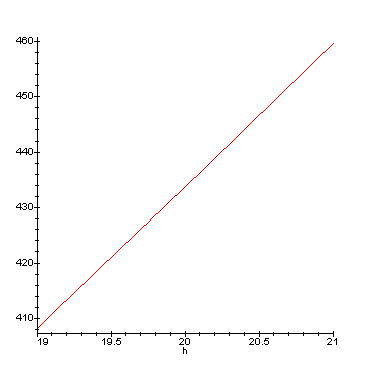
d h
v
24 19.0 408.3
24 19.1 410.8
24 19.2 413.3
...
Koska tilavuuden muutos pituuden muuttuessa on lähes lineaarista (läpimitan ollessa 24 cm), voidaan tehdä se päätelmä, että virhejakauman muoto likimain säilyy, jakauma vain skaalautuu uudelle välille.
Tilavuusestimaatit jakautuvat siten normaalisesti, odotusarvonaan 434 dm3 ja keskihajontanaan n. 25 dm3.
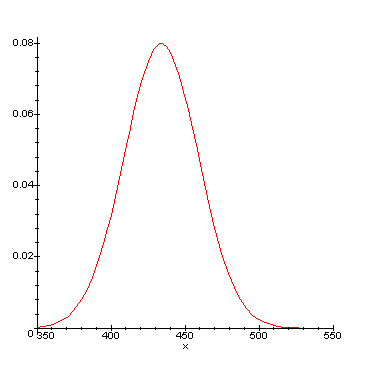 Tilavuus vaihteli ±
25 dm3 lineaarisesti, kun pituus vaihteli ±
1 m (joka oli keskihajonta)
Tilavuus vaihteli ±
25 dm3 lineaarisesti, kun pituus vaihteli ±
1 m (joka oli keskihajonta)
Normaalijakauman tiheysfunktio:
Odotusarvo 434, keskihajonta 25.
Jos puu sen sijaan on kallellaan, ja sitä mitataan satunnaisesti eri suunnista, aiheutuu tuloksiin harhaa, eikä jakauman keskikohta enää ole oikean arvon 434 dm3 kohdalla, vaan suurempi, ja jakauma on oikealle vino.
Otantavirhettä syntyy silloin, kun koko populaatio ei ole otoksessa. Esimerkin metsikkökuviota mitattaessa voidaan tyytyä esim. koealamittauksiin täysluvun sijaan, ja tällöin tuloksiin tulee lisää epävarmuutta. Tai sitten täysluvun yhteydessä kaikki puita (kaikki tunnukset eivät ole otoksessa) ei mitata koepuina, vaan vain osa - tällöinkin koepuiden otantaan sisältyy otantavirhettä.
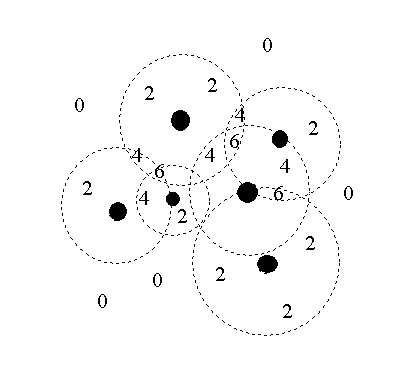 Esimerkkikuva siitä,
kuinka pohjapinta-alan otantavirhe syntyy.
Esimerkkikuva siitä,
kuinka pohjapinta-alan otantavirhe syntyy.
Tummat ympyrät ovat puita. Katkoviivalla piirretty ympyrä puun ympärillä kuvaa sitä sädettä, jonka sisältä puu tulee luetuksi relaskoopilla, kerroin 2.
Kun kyseisessä 'kuuden puun metsikössä' liikkuu ja tekee
relaskoopilla mittauksia, saa eri kohdista mitattaesaa erilaisia pohja-pinta-ala-arvoja,
joiden arvot vaihtelevat vällillä 0- 6 m2/ha.
Puiden todennäköisyys kuulua otokseen riippuu niiden koosta
(läpimitasta) relaskoopilla mitattaessa.
Samalla tavoin vaihtelevat myös muut metsikkötunnukset metsikön
sisällä (metsässä yleensä).

Kuvassa on 50 x 50 metrin mäntykoealan puukartta, jossa 'pallukat' kuvaavat puiden runkotilavuutta.
Vaaleat alueet koealakartan oikeassa reunassa ovat puuttomia kalliopaljastumia. Tässä kohtaa metsätyyppiä voisi kuvata VT-kiviseksi. Koealakartan vasen reuna kuvaa metsätyypiltään MT:tä muistuttavaa osaa metsää. Näkymä edustaa siis aluetta yhden metsikön sisällä (n. 1 ha, Hyytiälässä), puuston on noin 40-vuotiasta, kylvöalkuperää (viljelymetsä).
Katsotaan seuraavaksi, miltä kyseiselle koealalle simuloidut 1 aarin neliökoealojen tulokset eri metsikkömuutujien osalta näyttävät:
10 * 10 metrin koealaa liikutettiin kyseisessä metsikössä puoli metriä kerrallaan, ja aina pysähdyttäessä 'mitattiin koeala'. Havaintoja kertyy näin menetellen tuhansia jo varsin pienellekin alueelle.
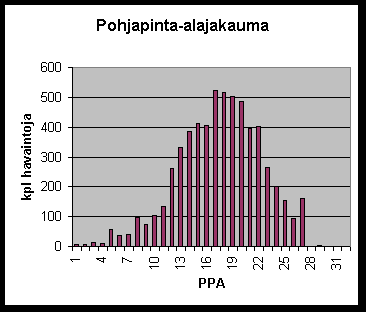
Saatujen tulosten histogrammi kertoo meille koealan (metsikön)
sisäisestä vaihtelusta käytettäessä 1 aarin neliökoealaa
pohjapinta-alan mittaukseen.
Tulokset painottuvat (odotusarvo) oikean arvon 18 m2/ha molemmille
puolille ja niistä muodostuva jakauma on lähes symmetrinen.
Jos koealaa suurennettaisiin, kuinka histogrammi muuttuisi ?
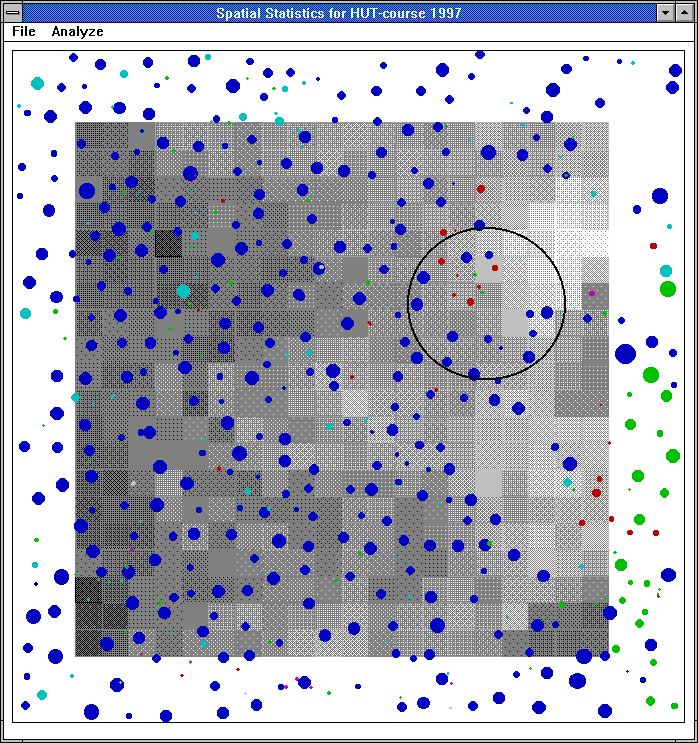
Kuvaan on harmaasävynä tulostettu kunkin 1 aarin ympyräkoealan
puiden runkotilavuus. Koealoja on 'ripoteltu systemaattisesti' 2 x 2 metrin
välein.
Kuvasta ilmenee periaate sille, miksi systemaattinen koealojen sijoittelu metsään satunnaista sijoittelua tehokkaampi.
Viereiset harmaasävyt muistuttavat toisiaan. Jos jossakin 2 x 2 metrin ruudun keskipisteestä arviooitu tilavuus on alhainen, on se sitä suurella todennäköisyydellä myös viereisessä pisteessä. Satunnainen koealojen sijoittelu metsikössä/metsäalueella voi aiheuttaa sen, että koealat sijaitsevat aivan toistensa vieressä, ja eivät 'tuo toisiinsa nähden' uutta informaatiota.