PUUANALYYSI
Esimerkki 1. Runkokäyrien
ja yksittäisen puun tilavuusmallien laatiminen
Olkoon MARV1-monisteen liitteen 1.2 puu esimerkkinä. Kyseinen mänty
on mitattu 1986 Hyytiälässä.
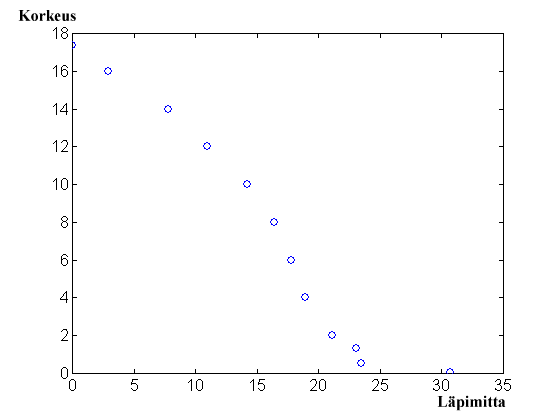 Piirretään
sen kuoren päältä mitatuista läpimitoista runkokäyrä:
Piirretään
sen kuoren päältä mitatuista läpimitoista runkokäyrä:
Mittaukset näyttävät melko loogisilta. 0.53 metrin korkeuden
havainto tosin hieman epäilyttää, mutta annetaan sen olla,
kun syytä havainnon hylkäämiseenkään ei ole. Puu
on 17.34 metriä pitkä. Laasasenahon runkokäyrät ennustavat
suhteellista läpimittaa dx/d.2h, eli runkokäyrä
kertoo, kuinka paljon läpimitta suhteellisesti poikkeaa läpimitasta
20 %:n korkeudella.Esimerkin puulla 20 %:n korkeus vastaa 3.47 metrin korkeutta.
Sieltä ei puuanalyysissä ole runkoa katkaistu, mutta arvioidaan
(interpoloidaan) tuo läpimitta samalla tekniikalla kuin Laasasenho
runkokäyriä laatiessaan, eli kuutiosplini-funktioilla.
Kun havainnot tasoittaa splini-funktioilla, saadaan ao. kuvan mukainen
'tasoituskäyrä'. (MATLAB)
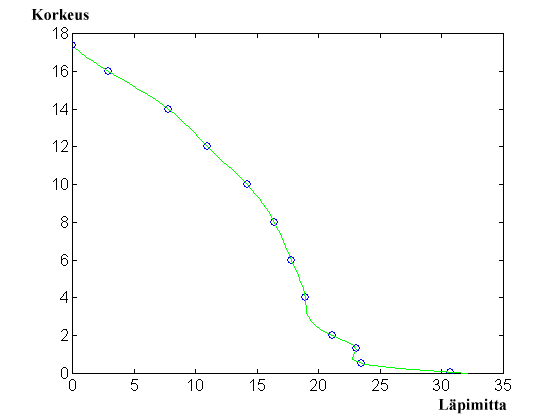 3.47 metrin
korkeudella läpimitta splineillä interpoloiden on 18.97 cm, mikä
tietysti tuntuu hieman epäloogiselta, kun se mittausten mukaan on
18.9 cm neljässä metrissä. Tuo virhe johtuu siitä,
että splinitasoitus pyrkii 'kauniisti' mukailemaan havaintoparvea,
ja niin tehdessään mutkii pisteestä toiseen. Hyväksytään
interpolaatio kuitenkin.
3.47 metrin
korkeudella läpimitta splineillä interpoloiden on 18.97 cm, mikä
tietysti tuntuu hieman epäloogiselta, kun se mittausten mukaan on
18.9 cm neljässä metrissä. Tuo virhe johtuu siitä,
että splinitasoitus pyrkii 'kauniisti' mukailemaan havaintoparvea,
ja niin tehdessään mutkii pisteestä toiseen. Hyväksytään
interpolaatio kuitenkin.
Laasasenahon runkokäyräpolynomissa on kahdeksan termiä.
Em. läpimittojen suhdetta ennustetaan suhteellisen korkeuden potensseilla.
Suhteeellinen korkeus on määritelty niin, että tyvellä
se on 1 ja latvassa 0. [kaava 1]:
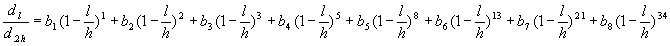
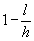 on suhteellisen
korkeuden muuttuja, joka saa siis puun tyvellä (syntypisteen / maanpinnan
tasolla) arvon 1 ja latvassa arvon 0 eli l on korkeus rungolla,
joka saa arvoja nollasta arvoon h. h siis on puun pituus.
on suhteellisen
korkeuden muuttuja, joka saa siis puun tyvellä (syntypisteen / maanpinnan
tasolla) arvon 1 ja latvassa arvon 0 eli l on korkeus rungolla,
joka saa arvoja nollasta arvoon h. h siis on puun pituus.
Laasasenahon polynomin kertoimet {b1,b2,..,b8}pitää
ratkaista kyseiselle puulle. Tuumaillaanpa niiden merkitystä ensin.
Kun ollaan tyvellä, saavat kaikki (1-l/h)- muuttujat
arvokseen yksi. Jotta malli toimisi, pitää kertoimien summan
b1+ b2+...+ b8 vastata tyven paksuuden
ja 20 %:n korkeuden paksuuden suhdetta. (joka on noin 1.5.) Latvaa kohti
mentäessä (1-l/h) -muuttujat lähestyvät
nollaa ja latvassa ovat nolla, joten malli toimii myös siellä,
koska läpimitta dl menee nollaan latvassa. Polynomissa
on sekä parittomia (1, 3, 5, 13, 21) että parillisia (2, 8, 34)
potensseja. Termi, jonka potenssi on 34, kuvaa rungon muodon muutosta vain
aivan tyvellä, koska mikrä tahansa luku nollan ja yhden välillä
korotettuna 34:een potenssiin on hyvin pieni luku (infiniittisen lähellä
nollaa), ellei olla aivan lähellä lukua yksi (eli tyvellä).
Alhaiset potenssitermit 1-8 määräävät yleisesti
runkokäyrän kulun ja korkeat termit (13,21,34) ohjailevat kulkua
vain aivan tyvellä, jossa niiden arvot ovat jotain muuta kuin äärimmäisen
lähellä nollaa.
Regressioanalyysillä ratkaisu (PNS-estimaatit):
Tehdään splini-tasoitetulta runkokäyrältä 100
kpl havaintoja tasavälein selitettävästä muuttujasta
(suhteellinen läpimitta) eri korkeuksilta (Y-muuttuja). Lasketaan
näiden sadan korkeuden potenssit 1,2,3,5,8,13,21 ja 34. Tehdään
niistä selittäviä muuttujia (Xi , kahdeksan kpl).
Ratkaistaan lineaarisen yhtälön [kaava 2]: Y
=
b1X1 + b2X2 + b3X3+...+b8X34
kertoimet.
Esimerkkipuulle ne ovat:
b1=2.0646,
b2=0.9644,
b3=-5.3643,
b4=8.4354,
b5=-11.1002,
b6=11.8042,
b7=-7.8388,
b8=2.7065
Kertoimien summa on 1.6718, mikä tarkoittaa sitä, että
runkokäyrä ennustaa tyven olevan 1.67 kertaa paksumpi kuin 20
%:n korkeuden.
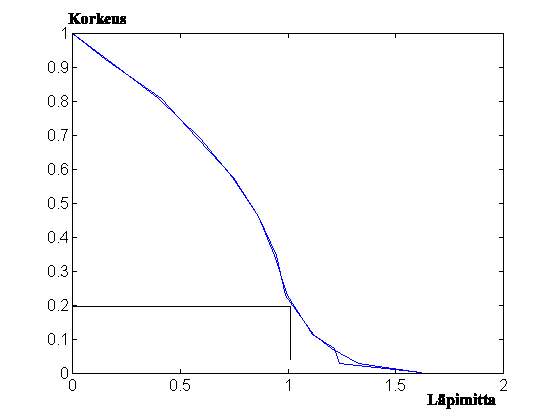 Piirretään
polynomirunkokäyrä ja havaittujen läpimittojen kautta kulkeva
runkokäyrä.
Piirretään
polynomirunkokäyrä ja havaittujen läpimittojen kautta kulkeva
runkokäyrä.
Kuvassa sileämpi käyrä vastaa laskettua polynomia ja
'kulmikkaampi' kulkee mittaushavaintojen kautta. Polynomi toteuttaa ehdon
'20 %:n korkeudella läpimittasuhde on 1'.
(Huom X-akseli käännetty Y-akseliksi.)
On saatu yhdellä puulla aikaiseksi runkokäyrä. Jos nyt
tehdään oletus, että kaikki Hyytiälän männyt
ovat riittävällä tarkkuudella kyseisen männyn 'muotoisia',
voidaan laatia 'tilavuusmalli'"
Lasketaan tilavuus esim. puulle, jonka läpimitta rinnankorkeudelta
on 16 cm ja pituus 14 m.
Ratkaistaan ensin 20 %:n korkeus. Se on 2,8 m. Sen ja 1,3 metrin korkeuden
läpimitan suhde on polynomilta ratkaistuna 1.164. Näin ollen
2,8 metrin korkeudella läpimitta on
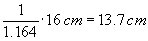 (Käänteisluku,
koska dl tiedosssa ja ratkaistaan d.2h
-muuttujaa) Nyt voidaan laskea tilavuus :
(Käänteisluku,
koska dl tiedosssa ja ratkaistaan d.2h
-muuttujaa) Nyt voidaan laskea tilavuus :
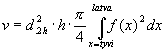 [kaava 3]
[kaava 3]
Yllä on pyörähdyskappaleen tilavuusintegraalin lauseke.
Kaava muistuttaa lukiomatematiikasta tuttua pyörähdyskappaleen
integraalia. Koska runkokäyrä kuvaa rungon suhteellista muutosta,
jolla ei ole mitään mittayksikköä, tarvitaan lausekkeessa
tekijät d2 [m2] ja h [m], jotta vastaukseksi
saadaan haluttua yksikköä [m3] oleva luku. f(x) on
runkokäyrä. x on integroimismuuttuja eli suhteellinen korkeus
tyveltä latvaan. x korvaa siis lausekkeen:
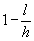
Kahdeksan termisen polynomin toisen potenssin laskeminen on paperilla
työlästä puuhaa. Potensseista 34, 21,...,1 kertyy erilaisia
sekatermejä yhteensä 30 kpl ja korkeimman termin asteluku nousee
68:een (34+34). Kun tämä korkea-asteinen ja moniterminen polynomi
vielä integroidaan, nousevat asteluvut vielä yhdellä.
hmm....integraali...
Otetaan harjoituksen vuoksi tähän väliin johto kartion
kaavalle: v = 1/3*g*h. Sitähän käytettiin
latvakappaleiden tilavuuden laskennassa.
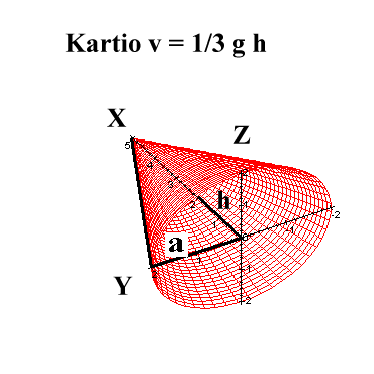 Kartio muodostuu
kun 'kolmio pyörähtää' x-akselin ympäri. Kolmion
kanta on a ja korkeus h. Hypotenuusan etäisyys x-akselista saadaan
kaavasta (hypotenuusa on 'runkokäyrä' ja etäisyys kertoo
kartion paksuuden d puolikkaan, säteen a = d/2 ) Kts. kuva. Älä
hätäänny, vaikka kuvassa säteelle käytetään
lyhennettä a "=" d/2).
Kartio muodostuu
kun 'kolmio pyörähtää' x-akselin ympäri. Kolmion
kanta on a ja korkeus h. Hypotenuusan etäisyys x-akselista saadaan
kaavasta (hypotenuusa on 'runkokäyrä' ja etäisyys kertoo
kartion paksuuden d puolikkaan, säteen a = d/2 ) Kts. kuva. Älä
hätäänny, vaikka kuvassa säteelle käytetään
lyhennettä a "=" d/2).
[kaava 4]:
 (et(x)
= kartion säde, korkeuden x = [0,h] funktiona)
(et(x)
= kartion säde, korkeuden x = [0,h] funktiona)
Kolmion kannalla x saa arvon nolla, joten etäisyys saa arvon a
ja kolmion kärjessä x saa arvon h, joten lausekkeesta tulee nolla.
Kaava on siis kartion 'runkokäyrä' (säteelle, ei läpimitalle
) , korotetaan se tilavuusintegraalin laskentaa varten toiseen potenssiin:
[kaava. 5]:
 Integroidaan x:n suhteen,
saadan integraalifunktio
Integroidaan x:n suhteen,
saadan integraalifunktio
[kaava 6]:

Lasketaan välillä x = [0,h] kartion
sisään jäävä tilavuus. Kerrotaan vielä tekijällä
p
(p = tulee siitä, että kartion pohjan
ala = p*r^2 ) Sijoituksia integraalifunktion
ylä- ja alarajalla ei tässä esitetä.
[kaava 7]:

Yhtälön oikea puoli vastaa kaavaa 1/3*g*h. Integraalissa 'laskettiin
differentiaalisen ohuiden et-säteisten kiekkojen tilavuus yhteen'.
Palataan laskemaan tilavuus 16 cm ja 14 m :lle männylle. Tässä
ei esitetä integraalilauseketta, joka saadaan kun em. kahdeksan terminen
polynomi korotetaan toiseen potenssin ja integroidaan välillä
0..1 (tyvi - latva). Todettakoon vain, että lausekkeessa on 30 termiä,
korkein potenssi 69 ja pienin 3. Moiset integroinnit on kätevintä
laskea jollakin matematiikkaohjelmistolla.
Runkokäyräpolynomin integraalin arvoksi välillä
0..1 saadaan kuitenkin 0.6828. Tämä luku on vakio kaikille puille,
joiden runko muistuttaa analyysipuumme runkomuotoa. Se vastaa 20 %:n korkeuden
muotolukua.
Kun tilavuus saadaan kaavalla v = f*g*h ja
meillä on tiedossa muotoluku 20 %:n korkeudelta, tarvitaan enää
g eli pohjapinta-ala kyseisellä korkeudella ja puun pituus.
Puun läpimitta 20 %:n korkeudella 13,7 cm vastaa ppa:ta 0,01474
m2. Pituus oli 14 m. Piin likiarvo 3.14.
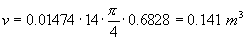
TTK:n taulukossa (mänty) vastaava kombinaatio d1.3 16
cm, 14 m antaa tilavuudeksi 142 litraa, joten puumme edusti melkolailla
maan keskiarvoa-muotoa tämän kokoiselle puulle.
Meillä on siis tilavuusmalli männyille v =
f.2h*g.2h*h, ja tarvittava f tiedossa sekä runkokäyrä,
jolla voidaan laskea läpimittoja eri korkeuksille runkoa. Runkokäyrää
voitaisiin edelleen käyttää monipuolisemmin, ja mm. muuntaa
poikkeuksellisen d,h -kombinaation ollessa kyseessä, kuten mm. PUUOSA
tekee (kts. Laasasenaho 1982, s. 29).
 Piirretään
sen kuoren päältä mitatuista läpimitoista runkokäyrä:
Piirretään
sen kuoren päältä mitatuista läpimitoista runkokäyrä:
 3.47 metrin
korkeudella läpimitta splineillä interpoloiden on 18.97 cm, mikä
tietysti tuntuu hieman epäloogiselta, kun se mittausten mukaan on
18.9 cm neljässä metrissä. Tuo virhe johtuu siitä,
että splinitasoitus pyrkii 'kauniisti' mukailemaan havaintoparvea,
ja niin tehdessään mutkii pisteestä toiseen. Hyväksytään
interpolaatio kuitenkin.
3.47 metrin
korkeudella läpimitta splineillä interpoloiden on 18.97 cm, mikä
tietysti tuntuu hieman epäloogiselta, kun se mittausten mukaan on
18.9 cm neljässä metrissä. Tuo virhe johtuu siitä,
että splinitasoitus pyrkii 'kauniisti' mukailemaan havaintoparvea,
ja niin tehdessään mutkii pisteestä toiseen. Hyväksytään
interpolaatio kuitenkin.
 Piirretään
polynomirunkokäyrä ja havaittujen läpimittojen kautta kulkeva
runkokäyrä.
Piirretään
polynomirunkokäyrä ja havaittujen läpimittojen kautta kulkeva
runkokäyrä.
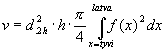 [kaava 3]
[kaava 3]
 Kartio muodostuu
kun 'kolmio pyörähtää' x-akselin ympäri. Kolmion
kanta on a ja korkeus h. Hypotenuusan etäisyys x-akselista saadaan
kaavasta (hypotenuusa on 'runkokäyrä' ja etäisyys kertoo
kartion paksuuden d puolikkaan, säteen a = d/2 ) Kts. kuva. Älä
hätäänny, vaikka kuvassa säteelle käytetään
lyhennettä a "=" d/2).
Kartio muodostuu
kun 'kolmio pyörähtää' x-akselin ympäri. Kolmion
kanta on a ja korkeus h. Hypotenuusan etäisyys x-akselista saadaan
kaavasta (hypotenuusa on 'runkokäyrä' ja etäisyys kertoo
kartion paksuuden d puolikkaan, säteen a = d/2 ) Kts. kuva. Älä
hätäänny, vaikka kuvassa säteelle käytetään
lyhennettä a "=" d/2).
 (et(x)
= kartion säde, korkeuden x = [0,h] funktiona)
(et(x)
= kartion säde, korkeuden x = [0,h] funktiona)
 Integroidaan x:n suhteen,
saadan integraalifunktio
Integroidaan x:n suhteen,
saadan integraalifunktio

