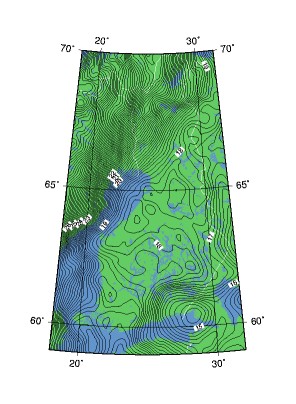
| On Coordinate systems In Hyytiälä we operate in the Finnish KKJ system that is a Gauss-Kruger map projection. For elevation (Z) we use the orthometric heights of the N60 system. Since KKJ is a map projection, it only approximates a true Cartesian (orthogonal) coordinate system. Also, the direction of the plumb-line, that is associated with orthometric heights, changes as we move on the map plane. In a small area we can consider the KKJ northing (P) as the Cartesian Y-axis, I as the X-axis and N60 heights as values of Z. The aerial photographs and the lidar data have been orientated in this type of "false" - "slight-violation-of" Cartesian 3D system. Objects measured from the aerial photographs get locally correct I, P and N60-values. KKJ is an old terrestrial coordinate system that dates back to the 1920s and it has been established by field triangulation. Nowadays, during the GPS-era, it is possible to obtain very accurate 3D coordinates in global coordinate systems. This has enabled to study the accuracy of KKJ, and it has turned out that the KKJ coordinate system has systematic errors: up to 2 meters in the north of Finland and 0-1 m in the south (Fig 1). The errors are locally correlated - they are trendlike phenomena (strecth). In Hyytiälä, there is an offset of about 0.5 m, if the "local stretch of KKJ" is not accounted for in transforming GPS-coordinates into KKJ-coordinates. This stretch is accounted for in the orientation of the image data and LiDAR, and must therefore be accounted for also in the transformation of GPS-observations into KKJ. Check that your GPS-receiver knows how to correct for the 0.5-m stretch. N60-values are elevations above sea level. They are measured in a gravity field that is not constant. GPS-elevations are, however, heights above a mathematical ellipsoid. The difference of the "sea level" and the ellipsoid surface in Hyytiälä is approximately 18.5 m. When GPS elevations are transformed into N60 ortometric heights, it is essential that the difference is known accurately. It is described by a geoid model (Fig. 2), and it has to be accurate in a GPS-receiver. |
Back to index,
Next
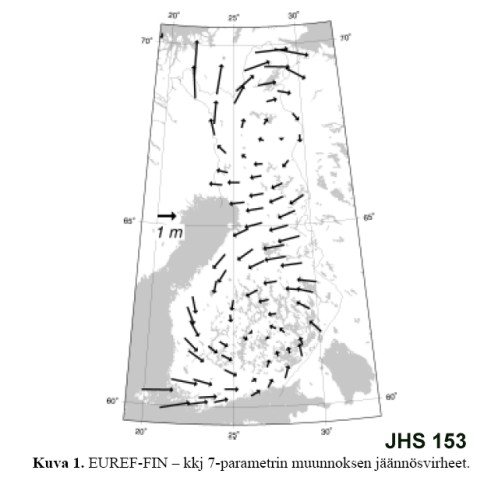
Fig. 1. The residuals of a standard 3D transformation
between GPS-observed coordinates (WGS-84/ETRS-89) and the KKJ. Source: Julkisen
hallinnon suositukset 153.
|