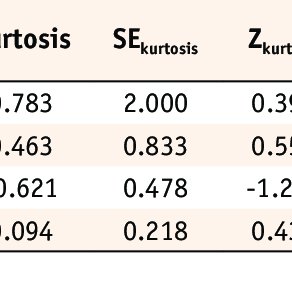
rde-38-52-normal-dist.pdf
Article
Statistical notes for clinical researchers: Assessing normal distribution (2) using skewness and kurtosis



271
0 new
Recommendations
0
0 new
667
29 new
Followers

1
0 new
ArticleStatistical notes for clinical researchers: Assessing normal distribution (2) using skewness and kurtosis
Abstract and figures
Figure content uploaded by Hae-Young Kim
Author content
Content uploaded by Hae-Young Kim
Author content
Similar research
The paper considers some properties of measures of asymmetry and peakedness of one dimensional distributions. It points to
some misconceptions of the first and the second Pearson coefficients, the measures of asymetry and shape, that frequently
occur in introductory textbooks. Also it presents different ways for obtaining the estimated values for the coefficients of
skewness and kurtosis and statistical tests which include them.
KeywordsSkewness-Kurtosis-Estimates of moments
We present results for the ratios of mean (MB), variance (σB2), skewness (SB) and kurtosis (κB) of net baryon-number fluctuations obtained in lattice QCD calculations with physical values of light and strange quark masses. Using next-to-leading order Taylor expansions in baryon chemical potential we find that qualitative features of these ratios closely resemble the corresponding experimentally measured cumulant ratios of net proton-number fluctuations for beam energies down to sNN≥19.6 GeV. We show that the difference in cumulant ratios for the mean net baryon-number, MB/σB2=χ1B(T,μB)/χ2B(T,μB), and the normalized skewness, SBσB=χ3B(T,μB)/χ2B(T,μB), naturally arises in QCD thermodynamics. Moreover, we establish a close relation between skewness and kurtosis ratios, SBσB3/MB=χ3B(T,μB)/χ1B(T,μB) and κBσB2=χ4B(T,μB)/χ2B(T,μB), valid at small values of the baryon chemical potential.
 Hae-Young Kim
Hae-Young Kim